题目内容
f(x)=x3+ax2+bx+a2在x=1有极值10,那么a+b的值为 ( )
| A.-7 | B.0? | C.-7或0 | D.不确定? |
A
∵f′(x)=3x2+2ax+b,由已知得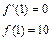
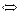
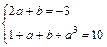
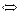
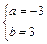
? 或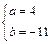 ,?
,?
当a=-3,b=3时,f ′(x)= 3(x-1)2≥0,此时x=1不是极值点.?
3(x-1)2≥0,此时x=1不是极值点.?
当a=4,b=-11时,易验证x=1是f(x)的极小值点,故选A.
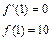
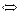
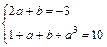
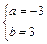
? 或
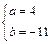 ,?
,?当a=-3,b=3时,f ′(x)=
 3(x-1)2≥0,此时x=1不是极值点.?
3(x-1)2≥0,此时x=1不是极值点.?当a=4,b=-11时,易验证x=1是f(x)的极小值点,故选A.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
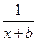 (a,b∈Z),曲线y=f(x)在点(2,f(2))处的切线方程为y=3。
(a,b∈Z),曲线y=f(x)在点(2,f(2))处的切线方程为y=3。 则称x0是f(x)的一个不动点.已知函数f(x)=ax2+(b+1)x+b-1(a≠0).
则称x0是f(x)的一个不动点.已知函数f(x)=ax2+(b+1)x+b-1(a≠0).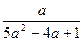 对称,求b的最小值.
对称,求b的最小值.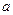
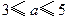
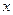
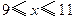
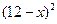
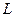 (万元)与每件产品的售价
(万元)与每件产品的售价 出
出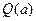
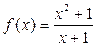
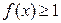 ;
;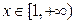 时,求函数
时,求函数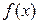 的最小值。
的最小值。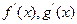 分别是f(x)、g(x)的导函数,且
分别是f(x)、g(x)的导函数,且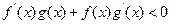 ,则当
,则当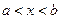 时,有( )
时,有( ) g(a)
g(a)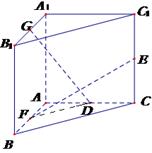
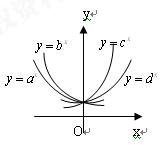
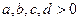 ,且不等于1,
,且不等于1,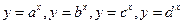 在同一坐标系中的图象如图,则
在同一坐标系中的图象如图,则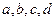 的大小顺序
的大小顺序  ( )
( )