题目内容
对于函数f（x），若存在区间[m，n]，使x∈[m，n]时，f（x）∈[km，kn]（k∈N*），则称区间[m，n]为函数f（x）的“k倍区间”．已知函数f（x）=x3+sinx，则的“5倍区间”的个数是（ ）
| A、0 | B、1 | C、2 | D、3 |
考点：函数的值域
专题：计算题,作图题,函数的性质及应用
分析：由题意可判断f（x）是R上的增函数，从而可知解x3+sinx=5x即可，作x3-5x，-sinx的图象，确定解的个数，从而求区间的个数．
解答：
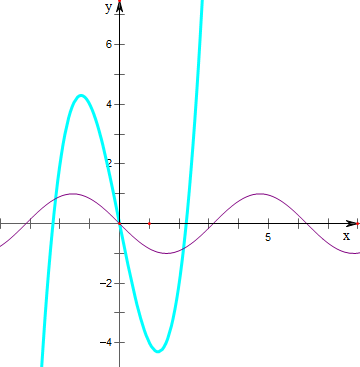解：∵f（x）=x3+sinx，
∴f′（x）=3x2+cosx＞0恒成立，
故f（x）是R上的增函数，
故令f（x）=5x，
即x3+sinx=5x，
即x3-5x=-sinx，
作x3-5x，-sinx的图象如图，
有三个交点，
函数f（x）=x3+sinx，则的“5倍区间”的个数是3个，
故选D．
解：∵f（x）=x3+sinx，∴f′（x）=3x2+cosx＞0恒成立，
故f（x）是R上的增函数，
故令f（x）=5x，
即x3+sinx=5x，
即x3-5x=-sinx，
作x3-5x，-sinx的图象如图，
有三个交点，
函数f（x）=x3+sinx，则的“5倍区间”的个数是3个，
故选D．
点评：本题考查了数形结合的应用，属于中档题．
练习册系列答案
相关题目
已知函数f（x）=x+
-2在区间（2，4）内有唯一零点，则b的取值范围是（ ）
| b |
| x |
| A、R |
| B、（-∞，0） |
| C、（-8，+∞） |
| D、（-8，0） |
若ξ～N（-1，σ2），且P（-3≤ξ≤-1）=0.4，则P（ξ≥1）等于（ ）
| A、0.1 | B、0.2 |
| C、0.3 | D、0.4 |
某次考试，班长算出了全班40人数学成绩的平均分M，如果把M当成一个同学的成绩与原来的40个分数加在一起，算出这41个分数的平均值为N，那么M；N为（ ）
| A、40：41 | B、41：40 |
| C、2 | D、1 |
设向量
=（-1，2）
=(2，-1)，则(
•
)(
+
)等于（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| A、（1，1） |
| B、（-4，-4） |
| C、-4 |
| D、（-2，-2） |