题目内容
已知数列{an}满足a1=1,an+1-an=4n-2(n∈N*),则使an≥163正整数n的最小值为 .
考点:数列递推式
专题:等差数列与等比数列
分析:根据累加法和等差数列的前n项和公式求出an,代入an≥163求出n的范围,再求出正整数n的最小值.
解答:
解:由题意得an+1-an=4n-2,
则当n≥2时,a2-a1=2,a3-a2=6,…,an-an-1=4n-6,
这n-1个式子相加,就有an-a1=
=2(n-1)2,
即an=2(n-1)2+1=2n2-4n+3,
当n=1时,a1=1也满足上式,所以an=2n2-4n+3,
由an≥163得2n2-4n+3≥163,即n2-2n-80≥0,
解得n≥10或n≤-8,所以n≥10,
即使an≥163正整数n的最小值为10,
故答案为:10.
则当n≥2时,a2-a1=2,a3-a2=6,…,an-an-1=4n-6,
这n-1个式子相加,就有an-a1=
| (n-1)(2+4n-6) |
| 2 |
即an=2(n-1)2+1=2n2-4n+3,
当n=1时,a1=1也满足上式,所以an=2n2-4n+3,
由an≥163得2n2-4n+3≥163,即n2-2n-80≥0,
解得n≥10或n≤-8,所以n≥10,
即使an≥163正整数n的最小值为10,
故答案为:10.
点评:本题考查了等差数列的前n项和公式,以及累加法求数列的通项公式,属于中档题.

练习册系列答案
相关题目
对于函数f(x),若存在区间[m,n],使x∈[m,n]时,f(x)∈[km,kn](k∈N*),则称区间[m,n]为函数f(x)的“k倍区间”.已知函数f(x)=x3+sinx,则的“5倍区间”的个数是( )
| A、0 | B、1 | C、2 | D、3 |
在△ABC中,若b=2,B=30°,C=135°,则a=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
△ABC的外接圆的圆心为O,半径为1,2
+
+
=
且|
|=|
|,则
•
的值等于( )
| OA |
| AB |
| AC |
| 0 |
| OA |
| AB |
| BA |
| BC |
| A、1 | ||
B、
| ||
| C、-1 | ||
D、-
|
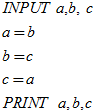 以下程序输入2,3,4运行后,输出的结果是
以下程序输入2,3,4运行后,输出的结果是