题目内容
对于函数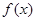 与
与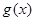 ,若区间
,若区间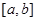 上
上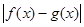 的最大值称为
的最大值称为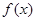 与
与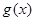 的“绝对差”,则
的“绝对差”,则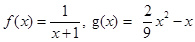 在
在 上的“绝对差”为
上的“绝对差”为
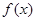 与
与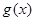 ,若区间
,若区间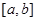 上
上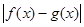 的最大值称为
的最大值称为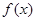 与
与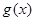 的“绝对差”,则
的“绝对差”,则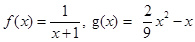 在
在 上的“绝对差”为
上的“绝对差”为A.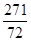 | B.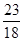 | C.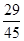 | D.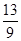 |
D
试题分析:构造函数
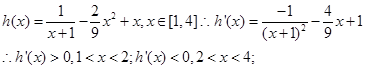
所以h(x)在[1,4]上先增后减.所以h(x)的最值在x=1或x=2或x=4处取得,且有
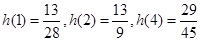 ,故有函数的绝对值差为
,故有函数的绝对值差为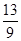 ,选D.
,选D.点评:解决此类问题的关键是利用求导公式正确求出函数的导数结合不等式的解法判断导数与0的大小,进而判断出函数的单调性即可得到函数的最值最终解决问题,利用导数求函数的最值是近年高考考查的重点

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
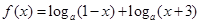 ,其中
,其中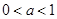 ,记函数
,记函数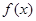 的定义域为D.
的定义域为D.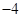 ,求
,求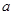 的值;
的值;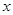 ,不等式
,不等式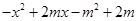 <
<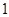 恒成立,求实数
恒成立,求实数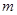 的取值范围.
的取值范围.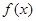 对定义域
对定义域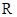 内的任意
内的任意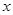 都有
都有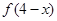 ,且当
,且当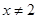 时其导函数
时其导函数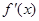 满足
满足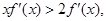 若
若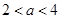 则
则
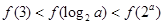
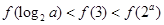
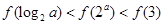
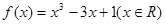 。
。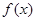 在点
在点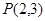 处的切线方程;
处的切线方程;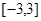 的最大值与最小值。
的最大值与最小值。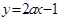 在[0,2]上的最大值是7,则指数函数
在[0,2]上的最大值是7,则指数函数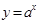 在[0,2]上的最大值与最小值的和为
在[0,2]上的最大值与最小值的和为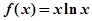 ,
,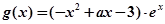 (其中
(其中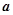 实数,
实数,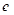 是自然对数的底数).
是自然对数的底数).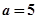 时,求函数
时,求函数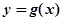 在点
在点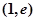 处的切线方程;
处的切线方程; 在区间
在区间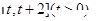 上的最小值;
上的最小值; ,使方程
,使方程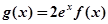 成立,求实数
成立,求实数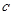 的取值范围.
的取值范围.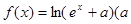 为常数,
为常数,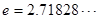 )是
)是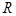 上的奇函数.
上的奇函数.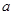 的值;(Ⅱ)讨论关于
的值;(Ⅱ)讨论关于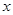 的方程
的方程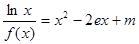 的根的个.
的根的个.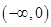 上单调递增的函数是 .
上单调递增的函数是 .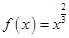 ②
②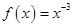 ③
③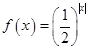 ④
④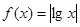
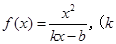 ,
,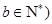 ,满足
,满足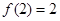 ,
,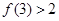 .
.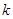 ,
,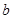 的值;
的值;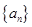 的前
的前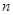 项和为
项和为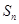 ,且有
,且有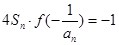 ,设
,设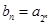 ,求数列
,求数列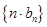 的前
的前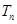 ;
;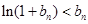 .
.