题目内容
设函数 ,且
,且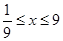 .
.
(1)求 的值;
的值;
(2)若令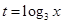 ,求
,求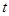 取值范围;
取值范围;
(3)将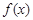 表示成以
表示成以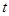 (
(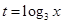 )为自变量的函数,并由此,求函数
)为自变量的函数,并由此,求函数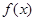 的最大值与最小值及与之对应的x的值.
的最大值与最小值及与之对应的x的值.
 ,且
,且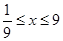 .
.(1)求
 的值;
的值;(2)若令
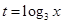 ,求
,求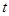 取值范围;
取值范围;(3)将
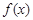 表示成以
表示成以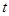 (
(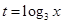 )为自变量的函数,并由此,求函数
)为自变量的函数,并由此,求函数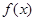 的最大值与最小值及与之对应的x的值.
的最大值与最小值及与之对应的x的值.(1)6(2)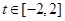 (3)
(3)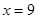
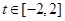 (3)
(3)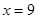
试题分析:解:(1).f(3)=
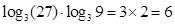 3分
3分(2).由
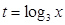 ,又
,又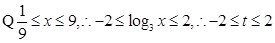 ..6分
..6分(3).由
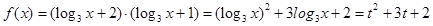 .8分
.8分令
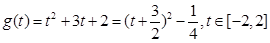 .9分
.9分1).当t=
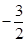 时,
时,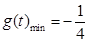 ,即
,即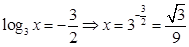 .
.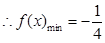 ,此时
,此时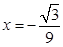 ..11分
..11分2).当t=2时,
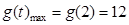 ,即
,即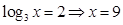 .
.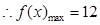 ,此时
,此时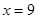 13分
13分点评:解决的关键是通过已知的函数的解析式来转化为二次函数来求解最值,属于基础题。

练习册系列答案
相关题目
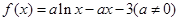 .
.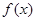 的单调区间
的单调区间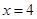 处切线的斜率为
处切线的斜率为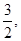 若函数
若函数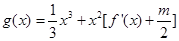 在区间(1,3)上不是单调函数,求m的取值范围
在区间(1,3)上不是单调函数,求m的取值范围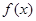 =
=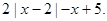
 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.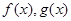 分别是定义在R上的奇函数和偶函数,当
分别是定义在R上的奇函数和偶函数,当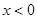 时,
时,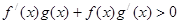 ,且
,且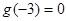 ,则
,则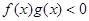 的解集是( )
的解集是( ) 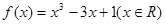 。
。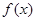 在点
在点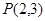 处的切线方程;
处的切线方程;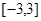 的最大值与最小值。
的最大值与最小值。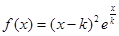 .
.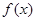 的单调区间;
的单调区间;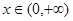 ,有
,有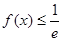 恒成立,求
恒成立,求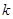 的取值范围.
的取值范围.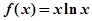 ,
,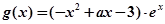 (其中
(其中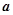 实数,
实数,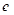 是自然对数的底数).
是自然对数的底数).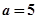 时,求函数
时,求函数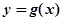 在点
在点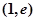 处的切线方程;
处的切线方程; 在区间
在区间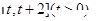 上的最小值;
上的最小值; ,使方程
,使方程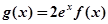 成立,求实数
成立,求实数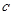 的取值范围.
的取值范围.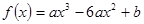 ,问是否存在实数
,问是否存在实数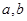 使
使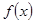 在
在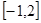 上取最大值3,最小值-29,若存在,求出
上取最大值3,最小值-29,若存在,求出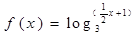 的单调递增区间为_______________.
的单调递增区间为_______________.