题目内容
已知复数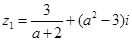 ,
, (
(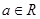 ,
,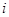 是虚数单位).
是虚数单位).
(1)若复数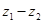 在复平面上对应点落在第一象限,求实数
在复平面上对应点落在第一象限,求实数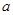 的取值范围;
的取值范围;
(2)若虚数 是实系数一元二次方程
是实系数一元二次方程 的根,求实数
的根,求实数 值.
值.
(1) ;(2)
;(2) .
.
解析试题分析:(1)先算出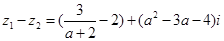 ,再根据
,再根据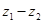 在复平面上对应的点落在第一象限,可得不等式组
在复平面上对应的点落在第一象限,可得不等式组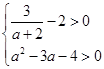 ,从中求解即可得出
,从中求解即可得出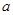 的取值范围;(2)根据实系数的一元二次方程有一复数根
的取值范围;(2)根据实系数的一元二次方程有一复数根 时,则该方程的另一个根必为
时,则该方程的另一个根必为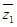 ,且
,且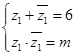 ,从而可先求解出
,从而可先求解出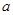 的值,进而求出
的值,进而求出 的值.
的值.
(1)由条件得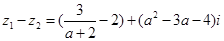 2分
2分
因为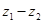 在复平面上对应点落在第一象限,故有
在复平面上对应点落在第一象限,故有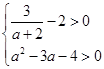 4分
4分
∴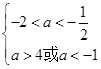 解得
解得 6分
6分
(2)因为虚数 是实系数一元二次方程
是实系数一元二次方程 的根,所以
的根,所以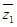 也是该方程的一个根
也是该方程的一个根
根据二次方程根与系数的关系可得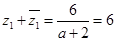 ,即
,即 10分
10分
把 代入,则
代入,则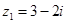 ,
, 11分
11分
所以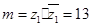 14分.
14分.
考点:1.复数的几何意义;2.实系数的一元二次方程在复数范围内根与系数的关系;3.复数的运算.

练习册系列答案
相关题目
 (
( )
) 是实数,求
是实数,求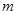 的值;
的值; 内,
内, ﹣a﹣bi|﹣2|z|=0,求z为何值时,|z|有最小值,并求出|z|的值.
﹣a﹣bi|﹣2|z|=0,求z为何值时,|z|有最小值,并求出|z|的值.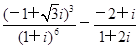 .?
.?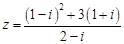 ,若
,若 ,
, ; (2)求实数
; (2)求实数 的值.
的值. =___________
=___________ =a,
=a,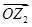 =b,求向量a与b的夹角.
=b,求向量a与b的夹角.