题目内容
已知复数z=(2+i)m2--2(1-i).当实数m取什么值时,复数z是:
(1)虚数;(2)纯虚数;(3)复平面内第二、四象限角平分线上的点对应的复数?
(1) m≠2且m≠1时,z为虚数;(2)m=- 时,z为纯虚数;(3) m=0或m=2时, z为复平面内第二、四象限角平分线上的点对应的复数.
时,z为纯虚数;(3) m=0或m=2时, z为复平面内第二、四象限角平分线上的点对应的复数.
解析试题分析:(1)复数z可表示为z=(2+i)m2﹣2(1﹣i)=2m2﹣2+(m2+2)i.只需令m2+2≠0即可;(2)只需2m2﹣2=0,且m2+2≠0即可;(3)只需2m2﹣2=﹣(m2+2)即可.
试题解析:由于m∈R,复数z可表示为z=(2+i)m2-3m(1+i)-2(1-i)=(2m2-3m-2)+(m2-3m+2)i.
(1)当m2-3m+2≠0,即m≠2且m≠1时,z为虚数.(3分)
(2)当即m=- 时,z为纯虚数.(3分)
时,z为纯虚数.(3分)
(3)当2m2-3m-2=-(m2-3m+2),即m=0或m=2时,z为复平面内第二、四象限角平分线上的点对应的复数.(4分)
考点:复数的基本概念.

练习册系列答案
相关题目
 为复数,
为复数, 为纯虚数,
为纯虚数, ,且
,且 ,求复数
,求复数 .
.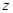 是复数,
是复数,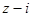 和
和 均为实数.
均为实数.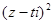 在复平面内对应点在第一象限,求实数t的取值范围.
在复平面内对应点在第一象限,求实数t的取值范围.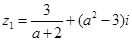 ,
, (
(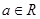 ,
,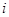 是虚数单位).
是虚数单位).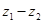 在复平面上对应点落在第一象限,求实数
在复平面上对应点落在第一象限,求实数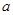 的取值范围;
的取值范围; 是实系数一元二次方程
是实系数一元二次方程 的根,求实数
的根,求实数 值.
值.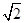 ,求z1.
,求z1. ,其中
,其中 为虚数单位,那么
为虚数单位,那么 = .
= . = _______________.
= _______________.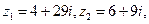 其中
其中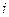 是虚数单位,则复数
是虚数单位,则复数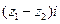 的实部为 ▲ 。
的实部为 ▲ 。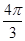 时,求|z|的值;
时,求|z|的值;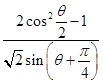 的值.
的值.