题目内容
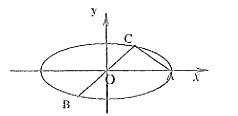
【题目】已知圆C过定点![]() ,且与直线
,且与直线![]() 相切,圆心C的轨迹为E,曲线E与直线l:
相切,圆心C的轨迹为E,曲线E与直线l:![]() (
(![]() )相交于A,B两点.
)相交于A,B两点.
(1)求曲线E的方程;
(2)当![]() 的面积等于
的面积等于![]() 时,求k的值.
时,求k的值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)点C到定点![]() 和直线
和直线![]() 的距离相等,可知点C的轨迹是抛物线,求出方程即可;
的距离相等,可知点C的轨迹是抛物线,求出方程即可;
(2)设直线l与x轴交于点N,可得![]() ,设
,设![]() ,
,![]() ,可得
,可得![]()
![]() ,然后将直线与抛物线方程联立并消去
,然后将直线与抛物线方程联立并消去![]() ,结合根与系数关系,可求得
,结合根与系数关系,可求得![]() ,进而可得到
,进而可得到![]() 的面积表达式,令其等于
的面积表达式,令其等于![]() ,可求出k的值.
,可求出k的值.
(1)由题意,点C到定点![]() 和直线
和直线![]() 的距离相等,故点C的轨迹是抛物线,
的距离相等,故点C的轨迹是抛物线,![]() 为焦点,
为焦点,![]() 为准线,故E的方程为
为准线,故E的方程为![]() .
.
(2)将直线方程与抛物线方程联立,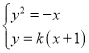 消去x,整理得
消去x,整理得![]() .设
.设![]() ,
,![]() ,
,
由根与系数关系![]() ,
,![]() .
.
设直线l与x轴交于点N,则![]() .
.
所以![]()
![]() .
.
因为![]() ,所以
,所以![]() .
.
故![]()
![]()
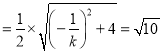 ,
,
解得![]() .
.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目