题目内容
【题目】已知双曲线过点(3,-2)且与椭圆4x2+9y2=36有相同的焦点.
(1)求双曲线的标准方程;
(2)若点M在双曲线上,F1,F2为左、右焦点,且|MF1|+|MF2|=6![]() ,试判别△MF1F2的形状.
,试判别△MF1F2的形状.
【答案】(1)![]() ; (2)钝角三角形.
; (2)钝角三角形.
【解析】
(1)设双曲线方程为![]() ,由题得
,由题得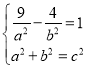 且c=
且c=![]() ,解方程组即得双曲线的标准方程.(2) 不妨设M点在右支上,则有|MF1|-|MF2|=2
,解方程组即得双曲线的标准方程.(2) 不妨设M点在右支上,则有|MF1|-|MF2|=2![]() ,求得|MF1|=4
,求得|MF1|=4![]() ,|MF2|=2
,|MF2|=2![]() ,|F1F2|=2
,|F1F2|=2![]() ,再利用余弦定理判定△MF1F2为钝角三角形.
,再利用余弦定理判定△MF1F2为钝角三角形.
(1)椭圆方程可化为![]() ,焦点在x轴上,且c=
,焦点在x轴上,且c=![]() ,
,
故设双曲线方程为![]() ,
,
则有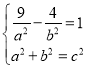 解得a2=3,b2=2.
解得a2=3,b2=2.
所以双曲线的标准方程为![]() .
.
(2)不妨设M点在右支上,
则有|MF1|-|MF2|=2![]() ,
,
又|MF1|+|MF2|=6![]() ,
,
故解得|MF1|=4![]() ,|MF2|=2
,|MF2|=2![]() ,
,
又|F1F2|=2![]() ,
,
因此在△MF1F2中,|MF1|边最长,而
cos ∠MF2F1=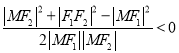 ,
,
所以∠MF2F1为钝角,故△MF1F2为钝角三角形.

练习册系列答案
相关题目