题目内容
【题目】椭圆![]() 过点
过点![]() ,离心率为
,离心率为![]() ,左右焦点分别为
,左右焦点分别为![]() ,过点
,过点![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() 两点。
两点。
(1)求椭圆![]() 的方程;
的方程;
(2)当![]() 的面积为
的面积为![]() 时,求直线
时,求直线![]() 的方程。
的方程。
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() 。
。
【解析】
(1)由已知条件推导出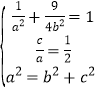 ,由此能求出椭圆C的方程.
,由此能求出椭圆C的方程.
(2)由(1)知F1(-1,0),①当l的倾斜角是![]() 时,
时,![]() ,不合题意;当l的倾斜角不是
,不合题意;当l的倾斜角不是![]() 时,设l的方程为
时,设l的方程为![]() ,由
,由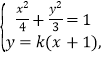 消去y得:
消去y得:![]() ,设A(x1,y1),B(x2,y2),由此利用韦达定理能求出直线l的方程.
,设A(x1,y1),B(x2,y2),由此利用韦达定理能求出直线l的方程.
(1)椭圆![]() 过点
过点![]()
离心率为![]()
又![]() ,解
,解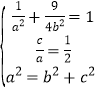 得
得![]()
![]() 椭圆C的方程
椭圆C的方程![]() .
.
(2)由(1)知![]() ,①当l的倾斜角是
,①当l的倾斜角是![]() 时,l的方程为
时,l的方程为![]() ,
,
交点![]() ,此时
,此时![]() ,不合题意;
,不合题意;
②当l的倾斜角不是![]() 时,设l的斜率为k,则其直线方程为
时,设l的斜率为k,则其直线方程为![]() ,
,
由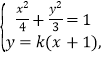 消去y得:
消去y得:![]() ,
,
设![]() ,则
,则![]() ,
,
![]()
![]()
![]()
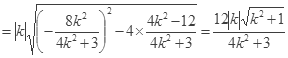 ,
,
又已知![]()
![]() ,
,
![]() 解得
解得![]() ,
,
故直线l的方程为![]() ,
,
即![]() 或
或![]() 。
。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】已知函数f(x)=|x+ ![]() |﹣|x﹣
|﹣|x﹣ ![]() |;
|;
(1)作出函数f(x)的图象;
(2)根据(1)所得图象,填写下面的表格:
性质 | 定义域 | 值域 | 单调性 | 奇偶性 | 零点 |
f(x) |
(3)关于x的方程f2(x)+m|f(x)|+n=0(m,n∈R)恰有6个不同的实数解,求n的取值范围.