题目内容
5.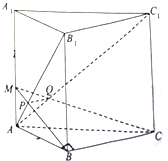 如图,已知三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥BC,且AB=$\sqrt{3}$,BC=4,AA1=3,M为棱AA1上的点,且AB1∩BM=P,AC1∩CM=Q.
如图,已知三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥BC,且AB=$\sqrt{3}$,BC=4,AA1=3,M为棱AA1上的点,且AB1∩BM=P,AC1∩CM=Q.(Ⅰ)若AM=$\frac{1}{3}$AA1,求PQ的长;
(Ⅱ)若AM=$\frac{1}{2}$AA1,求两面角A-PQ-B的余弦值.
分析 (Ⅰ)通过△AMP∽△B1BP、△AMQ∽△C1CQ即得结论;
(Ⅱ)易得APB即为二面角A-PQ-B的平面角,通过已知条件计算即可.
解答 解:(Ⅰ)根据题意,易得△AMP∽△B1BP,△AMQ∽△C1CQ,
又∵AM=$\frac{1}{3}$AA1,∴$AM=\frac{1}{3}B{B}_{1}=\frac{1}{3}C{C}_{1}$,
∴$\frac{MP}{PB}=\frac{AM}{B{B}_{1}}=\frac{1}{3}$,$\frac{MQ}{QC}=\frac{AM}{C{C}_{1}}=\frac{1}{3}$,
即△MPQ∽△MCB,
∴PQ∥BC,∴$\frac{PQ}{BC}=\frac{MQ}{MQ+QC}=\frac{1}{4}$,
又∵BC=4,
∴PQ=$\frac{1}{4}BC=\frac{1}{4}×4=1$;
(Ⅱ)∵A1A⊥BC,AB⊥BC,∴BC⊥平面ABB1A1,
又∵PQ∥BC,∴PQ⊥平面ABB1A1,
∴PQ⊥PA,PQ⊥PB,∴∠APB即为二面角A-PQ-B的平面角,
∵AB=$\sqrt{3}$,AA1=3,∴$A{B}_{1}=\sqrt{A{B}^{2}+B{{B}_{1}}^{2}}$=$\sqrt{3+{3}^{2}}$=$2\sqrt{3}$,
又∵AM=$\frac{1}{2}$AA1,∴BM=$\sqrt{A{M}^{2}+A{B}^{2}}$=$\sqrt{(\frac{3}{2})^{2}+3}$=$\frac{\sqrt{21}}{2}$,
∵△AMP∽△B1BP,
∴AP=$\frac{1}{3}A{B}_{1}$=$\frac{2\sqrt{3}}{3}$,BP=$\frac{2}{3}BM$=$\frac{\sqrt{21}}{3}$,
∴cos∠APB=$\frac{\frac{4}{3}+\frac{7}{3}-3}{2•\frac{2\sqrt{3}}{3}•\frac{\sqrt{21}}{3}}$=$\frac{\sqrt{7}}{14}$.
点评 本题考查二面角,相似三角形的性质,注意解题方法的积累,属于中档题.

| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
| A. | $[\frac{1}{2},2]$ | B. | [-1,3] | C. | $[-1,\frac{1}{2}]$ | D. | $[\frac{1}{2},1]$ |