题目内容
【题目】广元市某校高三数学备课组为了更好地制定二轮复习的计划,开展了试卷讲评后效果的调研,从上学期市一诊考试数学试题中选出一些学生易错题,重新进行测试,并认为做这些题不出任何错误的同学为“过关”,出了错误的同学为“不过关”,现随机抽查了年级![]() 人,他们的测试成绩的频数分布如下表:
人,他们的测试成绩的频数分布如下表:
市一诊分数段 |
|
|
|
|
|
人数 | 5 | 10 | 15 | 13 | 7 |
“过关”人数 | 1 | 3 | 8 | 8 | 6 |
(1)由以上统计数据完成如下![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为市一诊数学成绩不低于
的把握认为市一诊数学成绩不低于![]() 分与测试“过关”有关?说明你的理由;
分与测试“过关”有关?说明你的理由;
分数低于 | 分数不低于 | 合计 | |
“过关”人数 | |||
“不过关”人数 | |||
合计 |
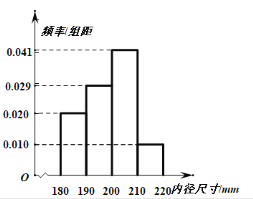
(2)根据以上数据估计该校市一诊考试数学成绩的中位数.下面的临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 |
| 2.072 | 2.706 | 3.841 | 5.024 |
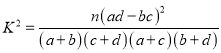
【答案】(1)填表见解析;有![]() 的把握认为期末数学成绩不低于
的把握认为期末数学成绩不低于![]() 分与测试“过关”有关,详见解析(2)中位数为
分与测试“过关”有关,详见解析(2)中位数为![]() 分
分
【解析】
(1)首先根据频数分布表中的数据填![]() 列联表,然后计算出
列联表,然后计算出![]() 即可;
即可;
(2)算出每个分数段的频率,然后即可算出中位数.
(1)根据题意得![]() 列联表如下:
列联表如下:
分数低于 | 分数不低于 | 合计 | |
“过关”人数 | 12 | 14 | 26 |
“不过关”人数 | 18 | 6 | 24 |
合计 | 30 | 20 | 50 |
所以,![]() .
.
因此有![]() 的把握认为期末数学成绩不低于
的把握认为期末数学成绩不低于![]() 分与测试“过关”有关.
分与测试“过关”有关.
(2)设该市一诊考试数学成绩的中位数为![]() .
.
市一诊分数段 |
|
|
|
|
|
人数 | 5 | 10 | 15 | 13 | 7 |
频率 | 0.1 | 0.2 | 0.3 | 0.26 | 0.14 |
根据题意有:![]() ,
,
解得:![]() .
.
所以,该校市一诊考试数学成绩的中位数为![]() 分.
分.

 名校课堂系列答案
名校课堂系列答案【题目】自由购是通过自助结算方式购物的一种形式. 某大型超市为调查顾客使用自由购的情况,随机抽取了100人,统计结果整理如下:
20以下 |
|
|
|
|
| 70以上 | |
使用人数 | 3 | 12 | 17 | 6 | 4 | 2 | 0 |
未使用人数 | 0 | 0 | 3 | 14 | 36 | 3 | 0 |
(Ⅰ)现随机抽取 1 名顾客,试估计该顾客年龄在![]() 且未使用自由购的概率;
且未使用自由购的概率;
(Ⅱ)从被抽取的年龄在![]() 使用自由购的顾客中,随机抽取3人进一步了解情况,用
使用自由购的顾客中,随机抽取3人进一步了解情况,用![]() 表示这3人中年龄在
表示这3人中年龄在![]() 的人数,求随机变量
的人数,求随机变量![]() 的分布列及数学期望;
的分布列及数学期望;
(Ⅲ)为鼓励顾客使用自由购,该超市拟对使用自由购的顾客赠送1个环保购物袋.若某日该超市预计有5000人购物,试估计该超市当天至少应准备多少个环保购物袋.