题目内容
【题目】已知F是抛物线C:x2=4y的焦点,过E(0,﹣1)的直线l与抛物线分別交于A,B两点.
(1)设直线AF,BF的斜率分別为k1,k2,证明:k1+k2=0;
(2)若![]() 的面积为
的面积为![]() ,求直线l的方程.
,求直线l的方程.
【答案】(1)见解析;(2)y=±2x﹣1.
【解析】
(1)当直线l的斜率为不存在时,易得不合题意;当直线l的斜率存在时,设直线l的方程为y=kx﹣1,A(x1,y1),B(x2,y2),与x2=4y联立,利用韦达定理以及斜率关系,化简即可得证;
(2)由题意![]() ,解得k,然后求出直线l的方程,即可得解.
,解得k,然后求出直线l的方程,即可得解.
(1)证明:当直线l的斜率为不存在时,l与抛物线只有一个交点,不合题意;
当直线l的斜率存在时,设直线l的方程为y=kx﹣1,A(x1,y1),B(x2,y2),
与x2=4y联立得:x2﹣4kx+4=0,![]() ,解得
,解得![]() 或
或![]() ,
,
则x1+x2=4k,x1x2=4,
抛物线C:x2=4y的焦点![]() ,
,
∴![]() ,
,
得证;
(2)由题意![]()
![]() ,
,
解得k=±2,
∴直线l的方程为:y=±2x﹣1.

【题目】广元市某校高三数学备课组为了更好地制定二轮复习的计划,开展了试卷讲评后效果的调研,从上学期市一诊考试数学试题中选出一些学生易错题,重新进行测试,并认为做这些题不出任何错误的同学为“过关”,出了错误的同学为“不过关”,现随机抽查了年级![]() 人,他们的测试成绩的频数分布如下表:
人,他们的测试成绩的频数分布如下表:
市一诊分数段 |
|
|
|
|
|
人数 | 5 | 10 | 15 | 13 | 7 |
“过关”人数 | 1 | 3 | 8 | 8 | 6 |
(1)由以上统计数据完成如下![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为市一诊数学成绩不低于
的把握认为市一诊数学成绩不低于![]() 分与测试“过关”有关?说明你的理由;
分与测试“过关”有关?说明你的理由;
分数低于 | 分数不低于 | 合计 | |
“过关”人数 | |||
“不过关”人数 | |||
合计 |
(2)根据以上数据估计该校市一诊考试数学成绩的中位数.下面的临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 |
| 2.072 | 2.706 | 3.841 | 5.024 |
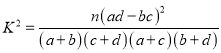
【题目】从某工厂的一个车间抽取某种产品50件,产品尺寸(单位:cm)落在各个小组的频数分布如下表:
数据分组 | [12.5,15.5) | [15.5,18.5) | [18.5,21.5) | [21.5,24.5) | [24.5,27.5) | [27.5,30.5) | [30.5,33.5) |
频数 | 3 | 8 | 9 | 12 | 10 | 5 | 3 |
(1)根据频数分布表,求该产品尺寸落在[27.5,33.5]内的概率;
(2)求这50件产品尺寸的样本平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(3)根据频数分布对应的直方图,可以认为这种产品尺寸![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为样本平均值
近似为样本平均值![]() ,
,![]() 近似为样本方差
近似为样本方差![]() ,经计算得
,经计算得![]() .利用该正态分布,求
.利用该正态分布,求![]() (
(![]() ).
).
附:(1)若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]()
![]() ;(2)
;(2)![]() .
.