题目内容
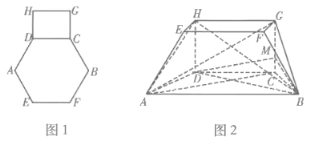
【题目】图1是由边长为4的正六边形![]() ,矩形
,矩形![]() ,组成的一个平面图形,将其沿
,组成的一个平面图形,将其沿![]() ,
,![]() 折起得几何体
折起得几何体![]() ,使得
,使得![]() ,且平面
,且平面![]() 平面
平面![]() ,如图2.
,如图2.
(1)证明:图2中,平面![]() 平面
平面![]() ;
;
(2)设点M为图2中线段![]() 上一点,且
上一点,且![]() ,若直线
,若直线![]() 平面
平面![]() ,求图2中的直线
,求图2中的直线![]() 与平面
与平面![]() 所成角的正弦值
所成角的正弦值
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)要证平面![]() 平面
平面![]() ,只需证
,只需证![]() 平面
平面![]() ,只需证
,只需证![]() 且
且![]() ,要证
,要证![]() ,只需证
,只需证![]() 平面
平面![]() ,只需证
,只需证![]() ,
,![]() .根据直线与平面垂直的判定与性质和平面与平面垂直的判定定理即可证得;
.根据直线与平面垂直的判定与性质和平面与平面垂直的判定定理即可证得;
(2)连接![]() 与
与![]() 交于点N,连接
交于点N,连接![]() ,利用线面平行的性质定理得到
,利用线面平行的性质定理得到![]() ,得到
,得到![]() ,再以
,再以![]() ,
,![]() ,
,![]() 分别作为x轴、y轴、z轴建立空间直角坐标系,利用向量法可求得直线
分别作为x轴、y轴、z轴建立空间直角坐标系,利用向量法可求得直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(1)证明:因为![]() 为矩形,所以
为矩形,所以![]() ,又
,又![]() ,
,![]() ,
,
所以![]() 平面
平面![]() ,故
,故![]() ,
,
因为![]() 为正六边形,所以
为正六边形,所以![]() ,
,
故![]() ,所以
,所以![]() ,即
,即![]() ,
,
又因为![]() ,所以
,所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
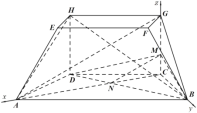
(2)解:连接![]() 与
与![]() 交于点N,连接
交于点N,连接![]() ,因为
,因为![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,
,
所以![]() ,所以
,所以![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
由(1)知;![]() ,
,![]() 平面
平面![]() ,故以
,故以![]() ,
,![]() ,
,![]() 分别作为x轴、y轴、z轴建立空间直角坐标系,如图:
分别作为x轴、y轴、z轴建立空间直角坐标系,如图:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,
设![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
则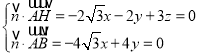 ,取
,取![]() ,则
,则![]() ,
,![]() ,所以
,所以![]() ,
,
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
所以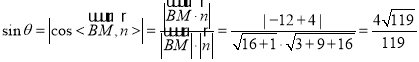 ,
,
即直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

 优学名师名题系列答案
优学名师名题系列答案【题目】广元市某校高三数学备课组为了更好地制定二轮复习的计划,开展了试卷讲评后效果的调研,从上学期市一诊考试数学试题中选出一些学生易错题,重新进行测试,并认为做这些题不出任何错误的同学为“过关”,出了错误的同学为“不过关”,现随机抽查了年级![]() 人,他们的测试成绩的频数分布如下表:
人,他们的测试成绩的频数分布如下表:
市一诊分数段 |
|
|
|
|
|
人数 | 5 | 10 | 15 | 13 | 7 |
“过关”人数 | 1 | 3 | 8 | 8 | 6 |
(1)由以上统计数据完成如下![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为市一诊数学成绩不低于
的把握认为市一诊数学成绩不低于![]() 分与测试“过关”有关?说明你的理由;
分与测试“过关”有关?说明你的理由;
分数低于 | 分数不低于 | 合计 | |
“过关”人数 | |||
“不过关”人数 | |||
合计 |
(2)根据以上数据估计该校市一诊考试数学成绩的中位数.下面的临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 |
| 2.072 | 2.706 | 3.841 | 5.024 |
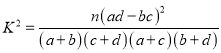
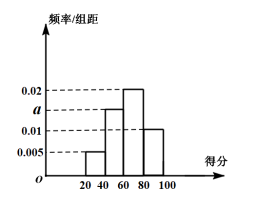
【题目】某校为了解校园安全教育系列活动的成效,对全校学生进行了一次安全意识测试,根据测试成绩评定“合格”“不合格”两个等级,同时对相应等级进行量化:“合格”记5分,“不合格”记0分.现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如下:
等级 | 不合格 | 合格 | ||
得分 |
|
|
|
|
频数 | 6 | a | 24 | b |
(1)由该题中频率分布直方图求测试成绩的平均数和中位数;
(2)其他条件不变在评定等级为“合格”的学生中依次抽取2人进行座谈,每次抽取1人,求在第1次抽取的测试得分低于80分的前提下,第2次抽取的测试得分仍低于80分的概率;
(3)用分层抽样的方法,从评定等级为“合格”和“不合格”的学生中抽取10人进行座谈.现再从这10人中任选4人,记所选4人的量化总分为![]() ,求
,求![]() 的数学期望
的数学期望![]() .
.