题目内容
(本小题满分12分)
数列{an}的前n项和为Sn,且a1=a,Sn+1=2Sn+n+1,n∈N*
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)当a=1时,若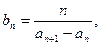 设数列{bn}的前n项和Tn,n∈N*,证明Tn<2。
设数列{bn}的前n项和Tn,n∈N*,证明Tn<2。
数列{an}的前n项和为Sn,且a1=a,Sn+1=2Sn+n+1,n∈N*
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)当a=1时,若
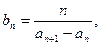 设数列{bn}的前n项和Tn,n∈N*,证明Tn<2。
设数列{bn}的前n项和Tn,n∈N*,证明Tn<2。解:
(Ⅰ)由Sn+1=2Sn+n+1 ①得
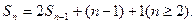 ②
②
①—②得

故 an+1=2an +1。(n≥2)···············································(2分)
又 an+1+1=2(an+1),
所以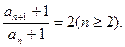
故数列{an+1}是从第2项其,以a2+1为首项,公比为2的等比数列。
又 S2=2S1+1+1,a1=a,所以a2=a+2。
故 an=(a+3)·2n-2-1(n≥2).
又a1=a不满足an=(a+3)·2n-2-1,
所以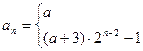
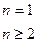 ····································6分
····································6分
(Ⅱ)由a1=1,得an==2n-1,n∈N*,则
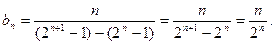
又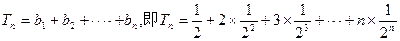 ①
①
得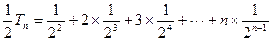 ②
②
①—②得
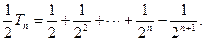
故
所以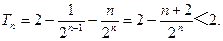 ································12分
································12分
(Ⅰ)由Sn+1=2Sn+n+1 ①得
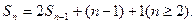 ②
②①—②得

故 an+1=2an +1。(n≥2)···············································(2分)
又 an+1+1=2(an+1),
所以
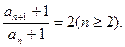
故数列{an+1}是从第2项其,以a2+1为首项,公比为2的等比数列。
又 S2=2S1+1+1,a1=a,所以a2=a+2。
故 an=(a+3)·2n-2-1(n≥2).
又a1=a不满足an=(a+3)·2n-2-1,
所以
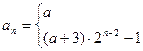
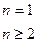 ····································6分
····································6分(Ⅱ)由a1=1,得an==2n-1,n∈N*,则
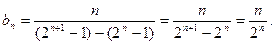
又
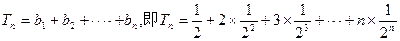 ①
①得
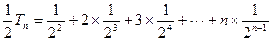 ②
②①—②得
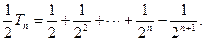
故

所以
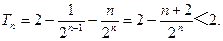 ································12分
································12分略

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
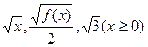 成等差数列.又数列
成等差数列.又数列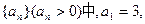 此数列的前n项的和Sn(
此数列的前n项的和Sn(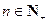 )对所有大于1的正整数n都有
)对所有大于1的正整数n都有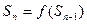 .
.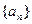 的第n+1项;
的第n+1项;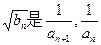 的等比中项,且Tn为{bn}的前n项和,求Tn.
的等比中项,且Tn为{bn}的前n项和,求Tn. 的前n项和为
的前n项和为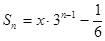 ,则x的值为
,则x的值为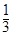
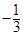
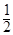
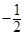
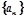 是公差不为0的等差数列,
是公差不为0的等差数列,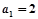 且
且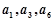 成等比数列,则
成等比数列,则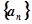 的前
的前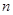 项和
项和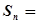
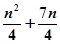
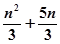
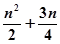
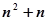
 的前
的前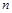 项和为
项和为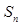 ,且
,且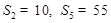 ,则过点
,则过点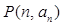 和
和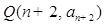
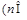 N*)的直线的斜率是
N*)的直线的斜率是 数列
数列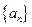 的前
的前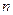 项和为
项和为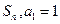 且
且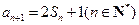 .
.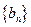 的各项均为正数,其前
的各项均为正数,其前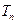 ,
,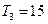 ,又
,又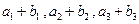 成等比数列,求
成等比数列,求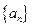 中,
中,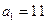 ,且
,且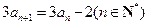 ,则该数列中相邻两项乘积的最小值为__________.
,则该数列中相邻两项乘积的最小值为__________.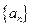 的前
的前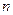 项和为
项和为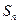 .已知
.已知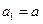 ,
,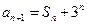 ,
,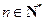 .
.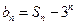 ,求数列
,求数列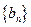 的通项公式;
的通项公式;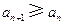 ,
,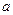 的取值范围.。
的取值范围.。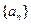 前n项和为
前n项和为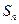 。若
。若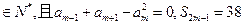 ,则m等于
,则m等于