题目内容
20.函数y=x3-x2-x的单调递减区间为($-\frac{1}{3}$,1).分析 先求出函数的导数,通过解导函数小于0,从而求出函数的递减区间.
解答 解:y′=3x2-2x-1,
令y′<0,解得:-$\frac{1}{3}$<x<1,
故答案为:(-$\frac{1}{3}$,1).
点评 本题考察了函数的单调性,导数的应用,是一道基础题.

练习册系列答案
相关题目
11.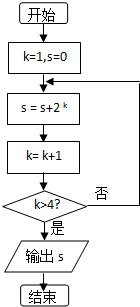 执行如图所示的程序框图,则输出s的值为( )
执行如图所示的程序框图,则输出s的值为( )
 执行如图所示的程序框图,则输出s的值为( )
执行如图所示的程序框图,则输出s的值为( )| A. | 30 | B. | 31 | C. | 62 | D. | 63 |
15.命题“关于x的不等式x2-ax+4>0在(0,+∞)上恒成立”的否定是( )
| A. | ?x∈(-∞,0),x2-ax+4>0 | B. | ?x∈(-∞,0),x2-ax+4>0 | ||
| C. | ?x∈(0,+∞),x2-ax+4≤0 | D. | ?x∈(0,+∞),x2-ax+4≤0 |
10.用反证法证明命题“若a,b为实数,则一元二次方程x2+bx+a=0没有实根”时,要做的假设正确的是( )
| A. | 方程x2+bx+a=0至多一个实根 | B. | 方程x2+bx+a=0有实根 | ||
| C. | 方程x2+bx+a=0至多有两个实根 | D. | 方程x2+bx+a=0恰好有两个实根 |