题目内容
【题目】已知函数![]() (其中e为自然对数的底).
(其中e为自然对数的底).
(1)若![]() 在
在![]() 上单调递增,求实数a的取值范围;
上单调递增,求实数a的取值范围;
(2)若![]() ,证明:
,证明:![]() 存在唯一的极小值点
存在唯一的极小值点![]() ,且
,且![]() .
.
【答案】(1)![]() ;(2)证明见解析
;(2)证明见解析
【解析】
(1)求导得![]() ,则
,则![]() 在
在![]() 时恒成立,不等式可转化为
时恒成立,不等式可转化为![]() ,求出
,求出![]() 的最小值,令
的最小值,令![]() 即可;
即可;
(2)![]() 时,
时,![]() ,求出导函数,可知
,求出导函数,可知![]() 单调递增,令
单调递增,令![]() ,易证
,易证![]() ,从而可证明
,从而可证明![]() 存在唯一的极小值点
存在唯一的极小值点![]() ,再结合
,再结合![]() ,可得到
,可得到![]() 和
和![]() ,从而可得到
,从而可得到![]() 的表达式,结合
的表达式,结合![]() ,求出
,求出![]() 的取值范围即可.
的取值范围即可.
(1)由题意,![]() ,则
,则![]() 在
在![]() 时恒成立,即
时恒成立,即![]() 在
在![]() 时恒成立,
时恒成立,
令![]() ,则
,则![]() ,显然
,显然![]() 在
在![]() 上单调递增,则
上单调递增,则![]() ,所以只需
,所以只需![]() ,即满足
,即满足![]() 在
在![]() 时恒成立,
时恒成立,
故实数a的取值范围是![]() .
.
(2)![]() ,则
,则![]() ,其定义域为
,其定义域为![]() ,
,
求导得![]() ,显然
,显然![]() 是
是![]() 上的增函数,
上的增函数,
![]() ,因为
,因为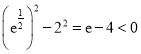 ,所以
,所以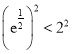 ,即
,即![]() ,
,
![]() ,因为
,因为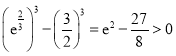 ,所以
,所以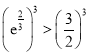 ,即
,即![]() ,
,
令![]() ,则
,则![]() 在
在![]() 上有唯一零点
上有唯一零点![]() ,且
,且![]() ,
,
故![]() 时,
时,![]() 单调递减,
单调递减,![]() 时,
时,![]() 单调递增,所以
单调递增,所以![]() 存在唯一的极小值点
存在唯一的极小值点![]() .
.
因为![]() ,所以
,所以![]() ,两边取对数得
,两边取对数得![]() ,即
,即![]() ,
,
故![]() ,
,![]() ,
,
构造函数![]() ,
,![]() ,
,
显然![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() ,
,
又![]() ,
,![]() ,故
,故![]() ,即
,即![]() .
.
所以![]() 存在唯一的极小值点
存在唯一的极小值点![]() ,且
,且![]() .
.

 走进文言文系列答案
走进文言文系列答案【题目】某校高三4班有50名学生进行了一场投篮测试,其中男生30人,女生20人.为了了解其投篮成绩,甲、乙两人分别都对全班的学生进行编号(1-50号),并以不同的方法进行数据抽样,其中一人用的是系统抽样,另一人用的是分层抽样.若此次投篮测试的成绩大于或等于80分视为优秀,小于80分视为不优秀,以下是甲、乙两人分别抽取的样本数据:
甲抽取的样本数据
编号 | 2 | 7 | 12 | 17 | 22 | 27 | 32 | 37 | 42 | 47 |
性别 | 男 | 女 | 男 | 男 | 女 | 男 | 女 | 男 | 女 | 女 |
投篮成 绩 | 90 | 60 | 75 | 80 | 83 | 85 | 75 | 80 | 70 | 60 |
乙抽取的样本数据
编号 | 1 | 8 | 10 | 20 | 23 | 28 | 33 | 35 | 43 | 48 |
性别 | 男 | 男 | 男 | 男 | 男 | 男 | 女 | 女 | 女 | 女 |
投篮成 绩 | 95 | 85 | 85 | 70 | 70 | 80 | 60 | 65 | 70 | 60 |
(Ⅰ)在乙抽取的样本中任取3人,记投篮优秀的学生人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
(Ⅱ)请你根据乙抽取的样本数据完成下列2×2列联表,判断是否有95%以上的把握认为投篮成绩和性别有关?
优秀 | 非优秀 | 合计 | |
男 | |||
女 | |||
合计 | 10 |
(Ⅲ)判断甲、乙各用何种抽样方法,并根据(Ⅱ)的结论判断哪种抽样方法更优?说明理由.
下面的临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
(参考公式: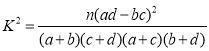 ,其中
,其中![]() )
)