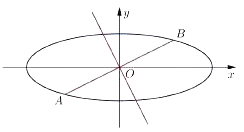
题目内容
【题目】已知曲线![]() 上任意一点
上任意一点![]() 到直线
到直线![]() :
:![]() 的距离是它到点
的距离是它到点![]() 距离的2倍;曲线
距离的2倍;曲线![]() 是以原点为顶点,
是以原点为顶点,![]() 为焦点的抛物线.
为焦点的抛物线.
(1)求![]() ,
,![]() 的方程;
的方程;
(2)设过点![]() 的动直线与曲线
的动直线与曲线![]() 相交于
相交于![]() ,
,![]() 两点,分别以
两点,分别以![]() ,
,![]() 为切点引曲线
为切点引曲线![]() 的两条切线
的两条切线![]() ,
,![]() ,设
,设![]() ,
,![]() 相交于点
相交于点![]() .连接
.连接![]() 的直线交曲线
的直线交曲线![]() 于
于![]() ,
,![]() 两点.
两点.
(i)求证:![]() ;
;
(ii)求![]() 的最小值.
的最小值.
【答案】(1)![]() 的方程为
的方程为![]() ,
,![]() 的方程为
的方程为![]() (2)(i)证明见解析(ii)
(2)(i)证明见解析(ii)![]()
【解析】
(1)根据几何特征列方程即可求解曲线方程;
(2)联立直线与曲线方程,结合韦达定理处理,(i)证明斜率之积为-1,(ii)化简代数式根据基本不等式求解最值.
(1)设![]() ,则由题意有
,则由题意有![]() ,化简得:
,化简得:![]() .
.
故![]() 的方程为
的方程为![]() ,
,
![]() 为抛物线的焦点,设其方程
为抛物线的焦点,设其方程![]() ,
,![]()
易知![]() 的方程为
的方程为![]() .
.
(2)(i)由题意可设![]() 的方程为
的方程为![]() ,代入
,代入![]() 得
得![]() ,
,
设![]() ,
,![]() ,则
,则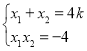 ,由
,由![]() 有
有![]() ,
,
所以![]() ,
,![]() 的方程分别为
的方程分别为![]() ,
,![]() .故
.故![]() ,
,
即![]() ,
,![]() ,从而
,从而![]() .
.
(ii)可设![]() 的方程为
的方程为![]() ,代入
,代入![]() 得
得
![]() ,设
,设![]() ,
,![]() ,
,
则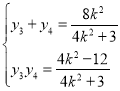 ,
,
所以![]()
![]()
![]()
![]()
![]()
![]()
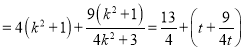 (其中
(其中![]() ).
).
设![]() ,则
,则![]() ,故
,故![]() 在
在![]() 单调递增,
单调递增,
因此![]() ,
,
当且仅当![]() 即
即![]() 等号成立.
等号成立.
故![]() 的最小值为7.
的最小值为7.

 阅读快车系列答案
阅读快车系列答案【题目】某企业为确定下一年度投入某种产品的生产所需的资金,需了解每投入2千万资金后,工人人数![]() (单位:百人)对年产能
(单位:百人)对年产能![]() (单位:千万元)的影响,对投入的人力和年产能的数据作了初步处理,得到散点图和统计量表.
(单位:千万元)的影响,对投入的人力和年产能的数据作了初步处理,得到散点图和统计量表.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
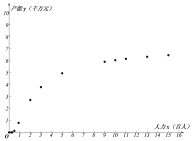
(1)根据散点图判断:![]() 与
与![]() 哪一个适宜作为年产能
哪一个适宜作为年产能![]() 关于投入的人力
关于投入的人力![]() 的回归方程类型?并说明理由?
的回归方程类型?并说明理由?
(2)根据(1)的判断结果及相关的计算数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)现该企业共有2000名生产工人,资金非常充足,为了使得年产能达到最大值,则下一年度共需投入多少资金(单位:千万元)?
附注:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为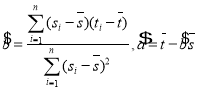 ,(说明:
,(说明:![]() 的导函数为
的导函数为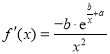 )
)
【题目】某医院体检中心为回馈大众,推出优惠活动:对首次参加体检的人员,按200元/次收费,并注册成为会员,对会员的后续体检给予相应优惠(本次即第一次),标准如下:
体检次序 | 第一次 | 第二次 | 第三次 | 第四次 | 第五次及以上 |
收费比例 | 1 | 0.95 | 0.90 | 0.85 | 0.8 |
该体检中心从所有会员中随机选取了100位对他们在本中心参加体检的次数进行统计,得到数据如下表:
体检次数 | 一次 | 两次 | 三次 | 四次 | 五次及以上 |
频数 | 60 | 20 | 12 | 4 | 4 |
假设该体检中心为顾客体检一次的成本费用为150元,根据所给数据,解答下列问题:
(1)已知某顾客在此体检中心参加了3次体检,求这3次体检,该体检中心的平均利润;
(2)该体检中心要从这100人里至少体检3次的会员中,按体检次数用分层抽样的方法抽出5人,再从这5人中抽取2人发放纪念品,求抽到的2人中恰有1人体检3次的概率.