题目内容
某工厂生产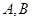 两种元件,其质量按测试指标划分为:大于或等于7.5为正品,小于7.5为次品.现从一批产品中随机抽取这两种元件各5件进行检测,检测结果记录如下:
两种元件,其质量按测试指标划分为:大于或等于7.5为正品,小于7.5为次品.现从一批产品中随机抽取这两种元件各5件进行检测,检测结果记录如下:
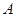 | 7 | 7 | 7.5 | 9 | 9.5 |
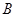 | 6 | 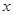 | 8.5 | 8.5 | 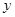 |
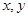 看不清,统计员只记得
看不清,统计员只记得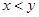 ,且
,且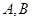 两种元件的检测数据的平均值相等,方差也相等.
两种元件的检测数据的平均值相等,方差也相等.(Ⅰ)求表格中
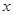 与
与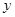 的值;
的值;(Ⅱ)若从被检测的5件
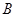 种元件中任取2件,求2件都为正品的概率.
种元件中任取2件,求2件都为正品的概率.
(Ⅰ)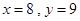 .(Ⅱ)
.(Ⅱ) 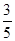 .
.
解析试题分析:(Ⅰ)因为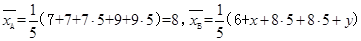 ,
,
由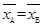 ,得
,得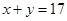 . ① 2分
. ① 2分
因为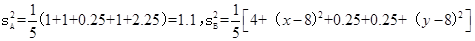 ,
,
由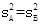 ,得
,得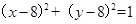 . ② 4分
. ② 4分
由①②解得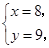 或
或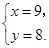 因为
因为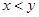 ,
,
所以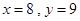 . 6分
. 6分
(Ⅱ) 记被检测的5件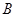 种元件分别为
种元件分别为 ,其中
,其中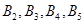 为正品,
为正品,
从中任取2件,共有10个基本事件,列举如下: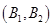 ,
,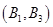 ,
,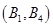 ,
,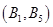 ,
,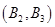 ,
,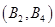 ,
,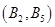 ,
,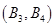 ,
,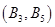 ,
,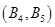 , 8分
, 8分
记“2件都为正品”为事件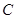 ,则事件
,则事件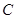 包含以下6个基本事件:
包含以下6个基本事件: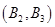 ,
,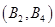 ,
,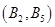 ,
,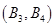 ,
,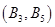 ,
,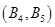 . 10分
. 10分
所以 ,即2件都为正品的概率为
,即2件都为正品的概率为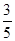 . 12分
. 12分
考点:本题考查了概率与统计
点评:在求概率时,应注意立事件概率公式的应用,还有区分是属于什么事件

练习册系列答案
相关题目
我区高三期末统一测试中某校的数学成绩分组统计如下表:
| 分组 | 频数 | 频率 |
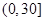 | 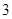 | 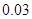 |
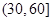 | 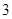 | 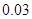 |
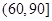 | 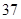 | 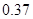 |
 | 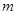 | 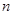 |
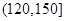 | 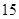 | 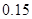 |
| 合计 | 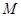 | 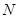 |
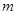 、
、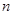 、
、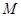 、
、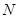 的值,并根据表中所给数据在下面给出的坐标系中画出频率分布直方图;
的值,并根据表中所给数据在下面给出的坐标系中画出频率分布直方图;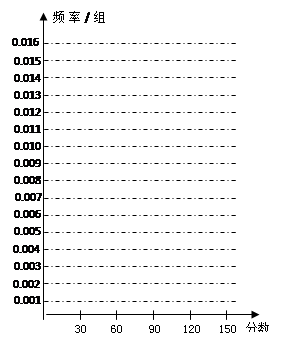
(2)若我区参加本次考试的学生有600人,试估计这次测试中我区成绩在
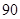 分以上的人数;
分以上的人数;(3)若该校教师拟从分数不超过60的学生中选取2人进行个案分析,求被选中2人分数不超过30分
的概率.
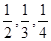 ,且每位同学能否通过考试时相互独立的。
,且每位同学能否通过考试时相互独立的。 ,求这三位同学中恰好有一位同学考上大学的概率。
,求这三位同学中恰好有一位同学考上大学的概率。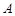 和
和 中装有若干个均匀的红球和白球,从
中装有若干个均匀的红球和白球,从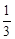 ,从
,从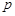 .
.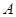 中有放回地摸球,每次摸出一个,共摸4次.
中有放回地摸球,每次摸出一个,共摸4次.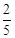 ,求
,求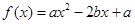 (
(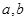
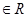 )
)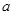 从集合
从集合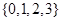 中任取一个元素,
中任取一个元素,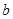 从集合
从集合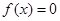 恰有两个不相等实根的概率;
恰有两个不相等实根的概率;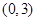 中任取一个数,
中任取一个数, 中任取一个数
中任取一个数 次,求在这一枪出现空弹的概率;
次,求在这一枪出现空弹的概率; 次,求在这三枪中出现空弹的概率;
次,求在这三枪中出现空弹的概率; 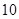 的等边
的等边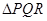 ,甲射手用实弹瞄准了三角形
,甲射手用实弹瞄准了三角形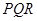 区域随机射击,且弹孔都落在三角形
区域随机射击,且弹孔都落在三角形