题目内容
我区高三期末统一测试中某校的数学成绩分组统计如下表:
| 分组 | 频数 | 频率 |
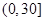 | 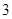 | 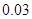 |
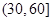 | 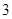 | 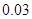 |
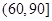 | 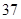 | 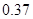 |
 | 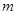 | 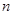 |
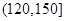 | 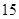 | 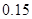 |
| 合计 |  |  |
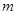 、
、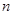 、
、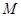 、
、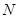 的值,并根据表中所给数据在下面给出的坐标系中画出频率分布直方图;
的值,并根据表中所给数据在下面给出的坐标系中画出频率分布直方图;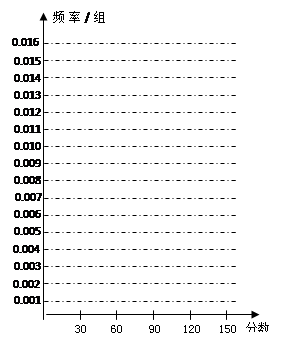
(2)若我区参加本次考试的学生有600人,试估计这次测试中我区成绩在
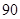 分以上的人数;
分以上的人数;(3)若该校教师拟从分数不超过60的学生中选取2人进行个案分析,求被选中2人分数不超过30分
的概率.
(1)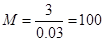 ,
, 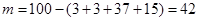 ,
,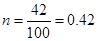 ,
,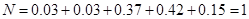 .
.
直方图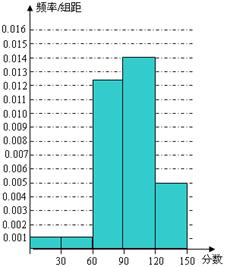 5分
5分
(2)全区90分以上学生估计为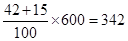 人.
人.
(3)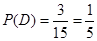 .
.
解析试题分析:(1)由频率分布表得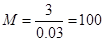 , 1分
, 1分
所以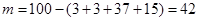 , 2分
, 2分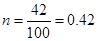 ,
,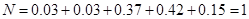 . 3分
. 3分
直方图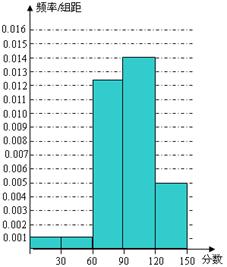 5分
5分
(2)由题意知,全区90分以上学生估计为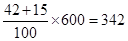 人. 7分
人. 7分
(3)设考试成绩在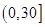 内的3人分别为A、B、C;
内的3人分别为A、B、C;
考试成绩在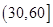 内的3人分别为a、b、c,
内的3人分别为a、b、c,
从不超过60分的6人中,任意抽取2人的结果有:
(A,B),(A,C),(A ,a),(A,b),(A,c),
(B,C),(B,a),(B,b),(B,c),(C,a),
(C,b),(C,c),(a,b),(a,c),(b,c)共有15个. 10分
设抽取的2人的分数均不大于30分为事件D.
则事件D含有3个结果: (A,B),(A,C) ,(B,C) 11分
∴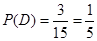 . 12分
. 12分
考点:本题主要考查频率分布表,频率分布直方图,频率的概念及计算,古典概型概率的计算。
点评:中档题,统计中的抽样方法,频率直方图,概率计算及分布列问题,是高考必考内容及题型。古典概型概率的计算问题,关键是明确基本事件数,往往借助于“树图法”,做到不重不漏。频率分布直方图中,小矩形的高等于每一组的频率÷组距,它们与频数成正比,小矩形的面积等于这一组的频率,则组距等于频率除以高。

设 和
和 分别是先后抛掷一枚骰子得到的点数,用随机变量
分别是先后抛掷一枚骰子得到的点数,用随机变量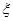 表示方程
表示方程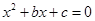 实根的个数(重根按一个计).
实根的个数(重根按一个计).
(1)求方程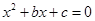 有实根的概率;
有实根的概率;
(2)求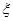 的分布列和数学期望;
的分布列和数学期望;
(3)求在先后两次出现的点数中有5的条件下,方程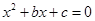 有实根的概率.
有实根的概率.
某工厂生产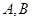 两种元件,其质量按测试指标划分为:大于或等于7.5为正品,小于7.5为次品.现从一批产品中随机抽取这两种元件各5件进行检测,检测结果记录如下:
两种元件,其质量按测试指标划分为:大于或等于7.5为正品,小于7.5为次品.现从一批产品中随机抽取这两种元件各5件进行检测,检测结果记录如下:
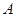 | 7 | 7 | 7.5 | 9 | 9.5 |
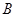 | 6 | 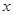 | 8.5 | 8.5 | 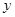 |
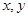 看不清,统计员只记得
看不清,统计员只记得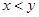 ,且
,且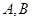 两种元件的检测数据的平均值相等,方差也相等.
两种元件的检测数据的平均值相等,方差也相等.(Ⅰ)求表格中
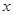 与
与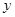 的值;
的值;(Ⅱ)若从被检测的5件
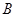 种元件中任取2件,求2件都为正品的概率.
种元件中任取2件,求2件都为正品的概率. 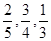 ,且假设各自能否被选中是无关的.
,且假设各自能否被选中是无关的.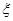 ,试求
,试求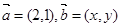
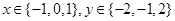 ,求向量
,求向量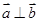 的概率;
的概率;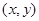 构成区域
构成区域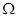 :
: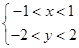 ,求二元数组
,求二元数组
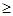 1的概率.
1的概率.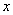 ,
,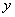 .现 从中任取3张卡片,假设每张卡片被取出的可能性相同.
.现 从中任取3张卡片,假设每张卡片被取出的可能性相同.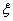 表示三张卡片上的数字之和.当三张卡片中含有字母时,则约定:有一个字母和二个相同数字时
表示三张卡片上的数字之和.当三张卡片中含有字母时,则约定:有一个字母和二个相同数字时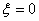 ,求
,求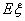 .
.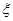 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求