题目内容
工商部门对甲、乙两家食品加工企业的产品进行深入检查后,决定对甲企业的5种产品和乙企业的3种产品做进一步的检验.检验员从以上8种产品中每次抽取一种逐一不重复地进行化验检验.
(1)求前3次检验的产品中至少1种是乙企业的产品的概率;
(2)记检验到第一种甲企业的产品时所检验的产品种数共为X,求X的分布列和数学期望.
(1)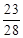
(2)
X的数学期望为:X 1 2 3 4 P 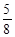
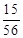
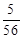
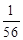
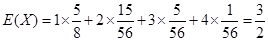
解析试题分析:解:(Ⅰ)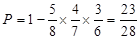 ,
,
∴ 前3次检验的产品中至少1种是乙企业的产品的概率为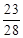 . 4分
. 4分
(Ⅱ) X可取值1,2,3,4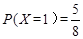 ,
, 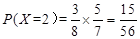 ,
,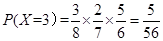 ,
,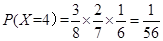 , 8分
, 8分
X的分布列如下表:
X的数学期望为:X 1 2 3 4 P 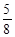
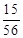
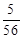
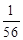
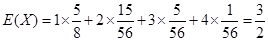 . 12分
. 12分
考点:独立事件的概率和分布列
点评:主要是考查了概率的运用,利用概率的乘法公式以及分布列的性质来求解,属于基础题。

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
设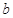 和
和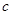 分别是先后抛掷一枚骰子得到的点数,用随机变量
分别是先后抛掷一枚骰子得到的点数,用随机变量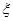 表示方程
表示方程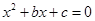 实根的个数(重根按一个计).
实根的个数(重根按一个计).
(1)求方程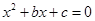 有实根的概率;
有实根的概率;
(2)求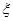 的分布列和数学期望;
的分布列和数学期望;
(3)求在先后两次出现的点数中有5的条件下,方程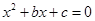 有实根的概率.
有实根的概率.
某工厂生产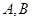 两种元件,其质量按测试指标划分为:大于或等于7.5为正品,小于7.5为次品.现从一批产品中随机抽取这两种元件各5件进行检测,检测结果记录如下:
两种元件,其质量按测试指标划分为:大于或等于7.5为正品,小于7.5为次品.现从一批产品中随机抽取这两种元件各5件进行检测,检测结果记录如下:
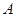 | 7 | 7 | 7.5 | 9 | 9.5 |
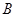 | 6 | 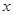 | 8.5 | 8.5 | 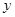 |
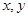 看不清,统计员只记得
看不清,统计员只记得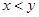 ,且
,且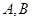 两种元件的检测数据的平均值相等,方差也相等.
两种元件的检测数据的平均值相等,方差也相等.(Ⅰ)求表格中
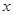 与
与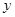 的值;
的值;(Ⅱ)若从被检测的5件
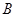 种元件中任取2件,求2件都为正品的概率.
种元件中任取2件,求2件都为正品的概率. 在某校高三学生的数学校本课程选课过程中,规定每位同学只能选一个科目。已知某班第一小组与第二小组各 有六位同学选择科目甲或科 目乙,情况如下表:
| | 科目甲 | 科目乙 | 总计 |
| 第一小组 | 1 | 5 | 6 |
| 第二小组 | 2 | 4 | 6 |
| 总计 | 3 | 9 | 12 |
(1)求选出的4 人均选科目乙的概率;
(2)设
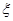 为选出的4个人中选科目甲的人数,求
为选出的4个人中选科目甲的人数,求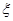 的分布列和数学期望.
的分布列和数学期望. 一家化妆品公司于今年三八节期间在某社区举行了为期三天的“健康使用化妆品知识讲座”.每位社区居民可以在这三天中的任意一天参加任何一个讨论,也可以放弃任何一个讲座(规定:各个讲座达到预先设定的人数时称为满座).统计数据表明,各个讲座各天满座的概率如下表:
| | 洗发水讲座 | 洗面奶讲座 | 护肤霜讲座 | 活颜营养讲座 | 面膜使用讲座 |
| 3月8日 | 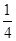 | 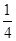 | 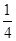 | 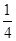 |  |
| 3月9日 |  |  |  |  | 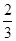 |
| 3月10日 | 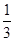 | 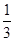 | 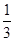 | 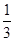 | 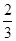 |
(2)设3月9日各个讲座满座的数目为
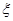 ,求随机变量
,求随机变量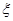 的分布列和数学期望.
的分布列和数学期望. 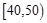 ,
,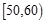 ,…,
,…,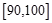 后得到如下频率分布直方图.
后得到如下频率分布直方图.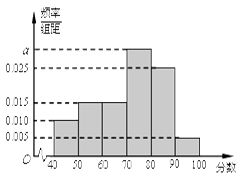
 的值
的值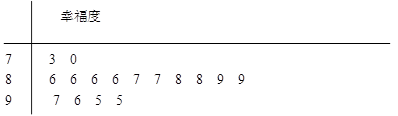
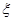 表示抽到“极幸福”的人数, 求
表示抽到“极幸福”的人数, 求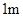 、
、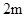 、
、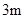 的钢管各
的钢管各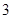 根(每根钢管质地均匀、粗细相同且附有不同的编号),从中随机抽取
根(每根钢管质地均匀、粗细相同且附有不同的编号),从中随机抽取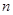 根(假设各钢管被抽取的可能性是均等的,
根(假设各钢管被抽取的可能性是均等的, ),再将抽取的钢管相接焊成笔直的一根.
),再将抽取的钢管相接焊成笔直的一根.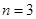 时,记事件
时,记事件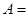 {抽取的
{抽取的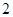 根长度相等},求
根长度相等},求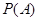 ;
;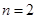 时,若用
时,若用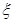 表示新焊成的钢管的长度(焊接误差不计),①求
表示新焊成的钢管的长度(焊接误差不计),①求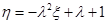 ,
,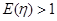 ,求实数
,求实数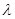 的取值范围.
的取值范围.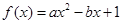 ,分别从集合P和Q中随机取一个数a和b得到数列
,分别从集合P和Q中随机取一个数a和b得到数列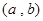 。
。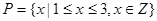 ,
,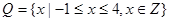 ,列举出所有的数对
,列举出所有的数对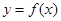 有零点的概率;
有零点的概率;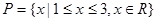 ,
,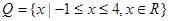 ,求函数
,求函数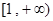 上是增函数的概率。
上是增函数的概率。