题目内容
(本小题满分12分)
甲打靶射击,有4发子弹,其中有一发是空弹(“空弹”即只有弹体没有弹头的子弹).
(1)如果甲只射击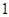 次,求在这一枪出现空弹的概率;
次,求在这一枪出现空弹的概率;
(2)如果甲共射击 次,求在这三枪中出现空弹的概率;
次,求在这三枪中出现空弹的概率;
(3)如果在靶上画一个边长为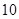 的等边
的等边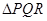 ,甲射手用实弹瞄准了三角形
,甲射手用实弹瞄准了三角形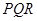 区域随机射击,且弹孔都落在三角形
区域随机射击,且弹孔都落在三角形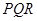 内。求弹孔与
内。求弹孔与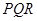 三个顶点的距离都大于1的概率(忽略弹孔大小).
三个顶点的距离都大于1的概率(忽略弹孔大小).
(1) 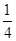 (2)
(2)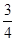 (3)
(3)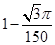
解析试题分析:设四发子弹编号为0(空弹),1,2,3。
(1)甲只射击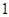 次,共有4个基本事件。
次,共有4个基本事件。
设第一枪出现“哑弹”的事件为A,则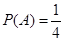 .
.
(2)甲共射击 次,前三枪共有4个基本事件:{0,1,2},{0,1,3},{0,2,3},{1,2,3};
次,前三枪共有4个基本事件:{0,1,2},{0,1,3},{0,2,3},{1,2,3};
设“甲共射击 次,这三枪中出现空弹”的事件为B,
次,这三枪中出现空弹”的事件为B,
B包含的的事件有三个:{0,1,2},{0,1,3},{0,2,3},
则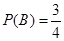 。
。
(3)等边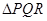 的面积为
的面积为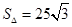 ,
,
分别以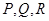 为圆心、1为半径的三个扇形的面积和为:
为圆心、1为半径的三个扇形的面积和为: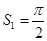 ,
,
设“弹孔与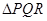 三个顶点的距离都大于1”的事件为C,
三个顶点的距离都大于1”的事件为C,
则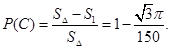
考点:本小题主要考查古典概型和集合概型的概率求解.
点评:本题考查古典概型、几何概型的计算,关键是理解、区分古典概型、几何概型两个不同的概念,并正确使用列举法求出基本事件的数目.

练习册系列答案
相关题目
某工厂生产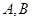 两种元件,其质量按测试指标划分为:大于或等于7.5为正品,小于7.5为次品.现从一批产品中随机抽取这两种元件各5件进行检测,检测结果记录如下:
两种元件,其质量按测试指标划分为:大于或等于7.5为正品,小于7.5为次品.现从一批产品中随机抽取这两种元件各5件进行检测,检测结果记录如下:
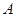 | 7 | 7 | 7.5 | 9 | 9.5 |
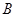 | 6 | 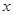 | 8.5 | 8.5 | 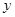 |
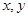 看不清,统计员只记得
看不清,统计员只记得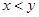 ,且
,且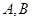 两种元件的检测数据的平均值相等,方差也相等.
两种元件的检测数据的平均值相等,方差也相等.(Ⅰ)求表格中
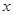 与
与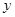 的值;
的值;(Ⅱ)若从被检测的5件
 种元件中任取2件,求2件都为正品的概率.
种元件中任取2件,求2件都为正品的概率. 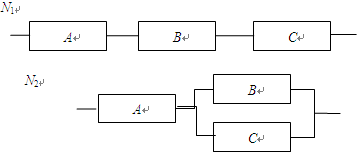
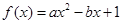 ,分别从集合P和Q中随机取一个数a和b得到数列
,分别从集合P和Q中随机取一个数a和b得到数列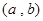 。
。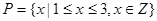 ,
,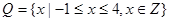 ,列举出所有的数对
,列举出所有的数对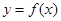 有零点的概率;
有零点的概率;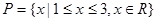 ,
,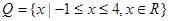 ,求函数
,求函数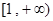 上是增函数的概率。
上是增函数的概率。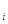 (
(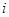 =1,2)表示方案
=1,2)表示方案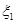 、
、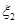 的分布列;
的分布列; 在R上不存在极值点的概率;
在R上不存在极值点的概率;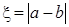 ,求
,求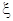 的分布列和数学期望.
的分布列和数学期望.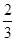 ,乙能攻克的概率为
,乙能攻克的概率为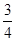 ,丙能攻克的概率为
,丙能攻克的概率为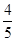 .
.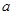 万元。奖励规则如下:若只有1人攻克,则此人获得全部奖金
万元。奖励规则如下:若只有1人攻克,则此人获得全部奖金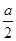 万元;若三人均攻克,则奖金奖给此三人,每人各得
万元;若三人均攻克,则奖金奖给此三人,每人各得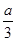 万元。设甲得到的奖金数为X,求X的分布列和数学期望。(本题满分12分)
万元。设甲得到的奖金数为X,求X的分布列和数学期望。(本题满分12分)