题目内容
一箱里有10件产品,其中3件次品,现从中任意抽取4件产品检查.
(1)求恰有1件次品的概率;
(2)求至少有1件次品的概率.
(1)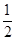 (2)
(2)
解析试题分析:(1)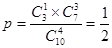 5分
5分
(2)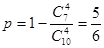 10分
10分
考点:古典概型概率
点评:古典概型概率的求解需找到所有基本事件的总数及满足题意要求的基本事件的种数,然后求其比值即可

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
某工厂生产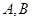 两种元件,其质量按测试指标划分为:大于或等于7.5为正品,小于7.5为次品.现从一批产品中随机抽取这两种元件各5件进行检测,检测结果记录如下:
两种元件,其质量按测试指标划分为:大于或等于7.5为正品,小于7.5为次品.现从一批产品中随机抽取这两种元件各5件进行检测,检测结果记录如下:
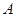 | 7 | 7 | 7.5 | 9 | 9.5 |
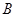 | 6 | 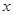 | 8.5 | 8.5 | 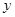 |
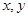 看不清,统计员只记得
看不清,统计员只记得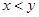 ,且
,且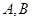 两种元件的检测数据的平均值相等,方差也相等.
两种元件的检测数据的平均值相等,方差也相等.(Ⅰ)求表格中
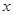 与
与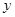 的值;
的值;(Ⅱ)若从被检测的5件
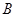 种元件中任取2件,求2件都为正品的概率.
种元件中任取2件,求2件都为正品的概率. 一家化妆品公司于今年三八节期间在某社区举行了为期三天的“健康使用化妆品知识讲座”.每位社区居民可以在这三天中的任意一天参加任何一个讨论,也可以放弃任何一个讲座(规定:各个讲座达到预先设定的人数时称为满座).统计数据表明,各个讲座各天满座的概率如下表:
| | 洗发水讲座 | 洗面奶讲座 | 护肤霜讲座 | 活颜营养讲座 | 面膜使用讲座 |
| 3月8日 | 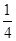 | 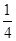 | 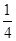 | 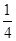 |  |
| 3月9日 |  |  |  |  | 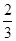 |
| 3月10日 | 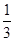 | 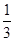 | 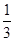 | 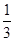 | 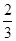 |
(2)设3月9日各个讲座满座的数目为
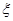 ,求随机变量
,求随机变量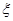 的分布列和数学期望.
的分布列和数学期望. 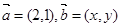
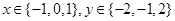 ,求向量
,求向量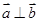 的概率;
的概率;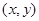 构成区域
构成区域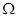 :
: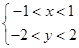 ,求二元数组
,求二元数组
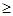 1的概率.
1的概率.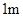 、
、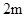 、
、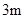 的钢管各
的钢管各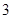 根(每根钢管质地均匀、粗细相同且附有不同的编号),从中随机抽取
根(每根钢管质地均匀、粗细相同且附有不同的编号),从中随机抽取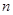 根(假设各钢管被抽取的可能性是均等的,
根(假设各钢管被抽取的可能性是均等的, ),再将抽取的钢管相接焊成笔直的一根.
),再将抽取的钢管相接焊成笔直的一根.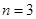 时,记事件
时,记事件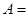 {抽取的
{抽取的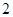 根长度相等},求
根长度相等},求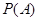 ;
;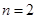 时,若用
时,若用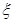 表示新焊成的钢管的长度(焊接误差不计),①求
表示新焊成的钢管的长度(焊接误差不计),①求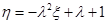 ,
,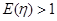 ,求实数
,求实数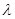 的取值范围.
的取值范围.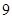 的
的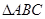 内任投一点
内任投一点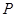 ,求
,求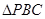 的面积小于
的面积小于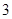 的概率?
的概率? 在R上不存在极值点的概率;
在R上不存在极值点的概率;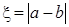 ,求
,求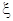 的分布列和数学期望.
的分布列和数学期望.