题目内容
【题目】直线l1 , l2分别是函数f(x)=sinx,x∈[0,π]图象上点P1 , P2处的切线,l1 , l2垂直相交于点P,且l1 , l2分别与y轴相交于点A,B,则△PAB的面积为 .
【答案】![]()
【解析】解:函数f(x)=sinx的导数为f′(x)=cosx,
设P1(x1,sinx1),P2(x2,sinx2),(设x1<x2),
可得图象上点P1,P2处的切线斜率为cosx1,cosx2,
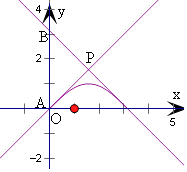
由l1,l2垂直,可得cosx1cosx2=﹣1,
由余弦函数的值域,可得cosx1=1,cosx2=﹣1,
即有x1=0,x2=π,
可得切线l1的方程为y=x,
l2的方程为y﹣0=﹣(x﹣π),即y=﹣x+π,
解得P( ![]() ,
, ![]() ),
),
由A(0,0),B(0,π),
可得△PAB的面积为 ![]() ×π×
×π× ![]() =
= ![]() .
.
所以答案是: ![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目