题目内容
【题目】已知函数f(x)= ![]() ,则y=f(x)的图象大致为( )
,则y=f(x)的图象大致为( )
A.
B.
C.
D.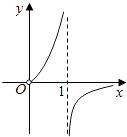
【答案】A
【解析】解:令g(x)=x﹣lnx﹣1,则 ![]() ,
,
由g'(x)>0,得x>1,即函数g(x)在(1,+∞)上单调递增,
由g'(x)<0得0<x<1,即函数g(x)在(0,1)上单调递减,
所以当x=1时,函数g(x)有最小值,g(x)min=g(0)=0,
于是对任意的x∈(0,1)∪(1,+∞),有g(x)≥0,故排除B、D,
因函数g(x)在(0,1)上单调递减,则函数f(x)在(0,1)上递增,故排除C,
故选A.
【考点精析】根据题目的已知条件,利用函数的图象和利用导数研究函数的单调性的相关知识可以得到问题的答案,需要掌握函数的图像是由直角坐标系中的一系列点组成;图像上每一点坐标(x,y)代表了函数的一对对应值,他的横坐标x表示自变量的某个值,纵坐标y表示与它对应的函数值;一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目