题目内容
2.已知x,y满足约束条件$\left\{\begin{array}{l}x<0\\ y>0\\ x+y-2≤0\\ x-y+4≥0\end{array}\right.$,若目标函数z=x+my(m≠0)取得最大值时最优解有无数个,则m的值为1.分析 画出满足约束条件的可行域,求出目标函数的最大值,从而建立关于m的等式,即可得出答案.
解答 解:由z=x+my得y=$-\frac{1}{m}$x$+\frac{z}{m}$,
若m>0,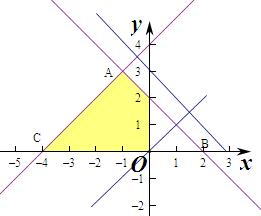
则目标函数的斜率k=$-\frac{1}{m}$<0,
作出不等式组对应的平面区域如图:
若目标函数z=x+my(m≠0)取得最大值时最优解有无数个,
由平移可知当直线y=$-\frac{1}{m}$x$+\frac{z}{m}$与AB平行时,满足条件,
此时$-\frac{1}{m}$=-1,解得m=1,
若m<0,则k=$-\frac{1}{m}$>0,
若目标函数z=x+my(m≠0)取得最大值时最优解有无数个,
则直线y=$-\frac{1}{m}$x$+\frac{z}{m}$,经过点0时,目标函数取得最大值,此时最大值只有一个,不满足条件.
故答案为:1
点评 本题主要考查线性规划的应用,根据目标函数的几何意义确定取得最大值的最优解是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.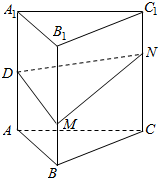 如图,正三棱柱ABC-A1B1C1(底面是正三角形,侧棱垂直底面)的各条棱长均相等,D为AA1的中点.M、N分别是BB1、CC1上的动点(含端点),且满足BM=C1N.当M,N运动时,下列结论中不正确的是( )
如图,正三棱柱ABC-A1B1C1(底面是正三角形,侧棱垂直底面)的各条棱长均相等,D为AA1的中点.M、N分别是BB1、CC1上的动点(含端点),且满足BM=C1N.当M,N运动时,下列结论中不正确的是( )
 如图,正三棱柱ABC-A1B1C1(底面是正三角形,侧棱垂直底面)的各条棱长均相等,D为AA1的中点.M、N分别是BB1、CC1上的动点(含端点),且满足BM=C1N.当M,N运动时,下列结论中不正确的是( )
如图,正三棱柱ABC-A1B1C1(底面是正三角形,侧棱垂直底面)的各条棱长均相等,D为AA1的中点.M、N分别是BB1、CC1上的动点(含端点),且满足BM=C1N.当M,N运动时,下列结论中不正确的是( )| A. | 平面DMN⊥平面BCC1B1 | |
| B. | 三棱锥A1-DMN的体积为定值 | |
| C. | △DMN可能为直角三角形 | |
| D. | 平面DMN与平面ABC所成的锐二面角范围为(0,$\frac{π}{4}$] |
 如图,点E,F分别在正方体ABCD-A1B1C1D1的棱DD1、AB上,下列命题:
如图,点E,F分别在正方体ABCD-A1B1C1D1的棱DD1、AB上,下列命题: