题目内容
8.已知数列{an}满足a1=5,a2=5,an+1=an+6an-1(n≥2)(1)求证:{an+1+2an}是等比数列
(2)求数列{an}的通项公式
(3)设3nbn=n(3n-an),求|b1|+|b2|+…+|bn|<m对于n∈N*恒成立,求m的取值范围.
分析 (1)由an+1=an+6an-1(n≥2),变形为an+1+2an=3(an+2an-1),又a2+2a1=15,利用等比数列的定义即可证明.
(2)由(1)可得:an+1+2an=15×3n-1=5×3n,变形为${a}_{n+1}-{3}^{n+1}=-2({a}_{n}-{3}^{n})$,利用等比数列的通项公式即可得出.
(3)由3nbn=n(3n-an),可得bn=n•$(-\frac{2}{3})^{n}$.|bn|=$n•(\frac{2}{3})^{n}$.令Sn=|b1|+|b2|+…+|bn|=$\frac{2}{3}+2×(\frac{2}{3})^{2}$+$3×(\frac{2}{3})^{3}$+…+$n•(\frac{2}{3})^{n}$,利用“错位相减法”与等比数列的前n项和公式即可得出.
解答 (1)证明:∵an+1=an+6an-1(n≥2),∴an+1+2an=3(an+2an-1),又a2+2a1=15,
∴{an+1+2an}是等比数列,首项为15,公比为3.
(2)解:由(1)可得:an+1+2an=15×3n-1=5×3n,变形为${a}_{n+1}-{3}^{n+1}=-2({a}_{n}-{3}^{n})$,
∴数列$\{{a}_{n}-{3}^{n}\}$是等比数列,首项为2,公比为-2,
∴${a}_{n}-{3}^{n}$=2×(-2)n-1,∴an=3n-(-2)n.
(3)解:3nbn=n(3n-an),∴3nbn=n•(-2)n,∴bn=n•$(-\frac{2}{3})^{n}$.
∴|bn|=$n•(\frac{2}{3})^{n}$.
令Sn=|b1|+|b2|+…+|bn|=$\frac{2}{3}+2×(\frac{2}{3})^{2}$+$3×(\frac{2}{3})^{3}$+…+$n•(\frac{2}{3})^{n}$,
∴$\frac{2}{3}{S}_{n}$=$(\frac{2}{3})^{2}+2×(\frac{2}{3})^{3}$+…+(n-1)$•(\frac{2}{3})^{n}$+$n•(\frac{2}{3})^{n+1}$,
两式相减可得:$\frac{1}{3}{S}_{n}$=$\frac{2}{3}$+$(\frac{2}{3})^{2}$+…+$(\frac{2}{3})^{n}$-$n•(\frac{2}{3})^{n+1}$=$\frac{\frac{2}{3}[1-(\frac{2}{3})^{n}]}{1-\frac{2}{3}}$-$n•(\frac{2}{3})^{n+1}$=2-$\frac{6+2n}{3}$$•(\frac{2}{3})^{n}$,
∴Sn=6-$(6+2n)•(\frac{2}{3})^{n}$.
要使|b1|+|b2|+…+|bn|<m对于n∈N*恒成立,
则m≥6.
∴m的取值范围是[6,+∞).
点评 本题考查了等比数列的定义通项公式及其前n项和公式、“错位相减法”、数列的单调性,考查了变形能力、推理能力与计算能力,属于中档题.

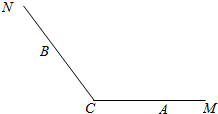 已知点A,B分别在射线CM,CN(不含端点C)上运动,∠MCN=$\frac{2π}{3}$,在△ABC中,角A,B,C所对的边分别是a,b,c
已知点A,B分别在射线CM,CN(不含端点C)上运动,∠MCN=$\frac{2π}{3}$,在△ABC中,角A,B,C所对的边分别是a,b,c