题目内容
【题目】已知动点
到定直线
：
的距离比到定点
的距离大2.
（1）求动点的轨迹
的方程；
（2）在
轴正半轴上，是否存在某个确定的点
，过该点的动直线与曲线交于
，
两点，使得
为定值.如果存在，求出点坐标；如果不存在，请说明理由.
【答案】（1）
（2）
【解析】分析：（1）利用抛物线定义即可求得抛物线方程；
（2）假设存在满足条件的点M（m，0）（m＞0），直线l：x=ty+m，有
，y2﹣8ty﹣8m=0，设A（x1，y1），B（x2，y2），利用韦达定理弦长公式，化简求解即可．
详解: （1）设点
的坐标为
，因为动点到定直线
：
的距离比到定点
的距离大2，所以
且
，
化简得，所以轨迹
的方程为.
（2）假设存在满足条件的点
（
），直线：
，
有
，
设
，
，有
，
，
，
，
，
据题意，
为定值，则
，
于是
，则有
解得
，
故当时，为定值
，所以
.
练习册系列答案
中考解读考点精练系列答案
相关题目
【题目】某高三理科班共有
名同学参加某次考试，从中随机挑出
名同学，他们的数学成绩
与物理成绩
如下表：
数学成绩 |
|
|
|
|
|
物理成绩 |
|
|
|
|
|
（1）数据表明与之间有较强的线性关系，求关于的线性回归方程；
（2）本次考试中，规定数学成绩达到
分为优秀，物理成绩达到
分为优秀.若该班数学优秀率与物理优秀率分别为
和
，且除去抽走的名同学外，剩下的同学中数学优秀但物理不优秀的同学共有人，请写出
列联表，判断能否在犯错误的概率不超过
的前提下认为数学优秀与物理优秀有关？
参考数据：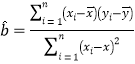
，
；
，
；
