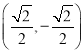ЬтФПФкШн
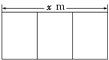
ЁОЬтФПЁП ЮЊСЫОЛЛЏЙужнЫЎЯЕЃЌФтдкаЁЧхКгНЈвЛзљЦНУцЭМ(ШчЭМЫљЪО)ЮЊОиаЮЧвУцЛ§ЮЊ200 m2ЕФШ§МЖЮлЫЎДІРэГиЃЌгЩгкЕиаЮЯожЦЃЌГЄЁЂПэЖМВЛФмГЌЙ§16 mЃЌШчЙћГиЭтБкНЈдьЕЅМлЮЊ400дЊ/m2ЃЌжаМфСНЬѕИєЧННЈдьЕЅМлЮЊ248дЊ/m2ЃЌГиЕзНЈдьЕЅМлЮЊ80дЊ/m2(ГиБкКёЖШКіТдВЛМЦЃЌЧвГиЮоИЧ)ЃЎ
(1)аДГізмдьМлy(дЊ)гыxЕФКЏЪ§ЙиЯЕЪНЃЌВЂжИГіЖЈвхгђЃЛ
(2)ЧѓЮлЫЎДІРэГиЕФГЄКЭПэИїЮЊЖрЩйЪБЃЌЮлЫЎДІРэГиЕФзмдьМлзюЕЭЃЌВЂЧѓзюЕЭдьМлЃЎ
ЁОД№АИЁП(1) yЃН800xЃЋ![]() ЃЋ16 000ЃЌ
ЃЋ16 000ЃЌ![]() ЁмxЁм16.
ЁмxЁм16.
(2) ЕБГЄЮЊ16 mЃЌПэЮЊ12.5 mЪБЃЌзмдьМлyзюЕЭЃЌЮЊ45 000дЊЃЎ
ЁОНтЮіЁП
ЪдЬтЃЈ1ЃЉЯШЧѓУцЛ§ЃЌдйГЫвдЖдгІМлИёЃЌЧѓКЭЕУзмдьМлЃЌИљОнГЄЁЂПэЖМВЛФмГЌЙ§16 mвЊЧѓШЗЖЈЖЈвхгђЃЈ2ЃЉРћгУЕМЪ§ПЩЕУКЏЪ§ЮЊЖЈвхгђЩЯЕЅЕїМѕКЏЪ§ЃЌдйИљОнЕЅЕїадЧѓзюаЁжЕ
ЪдЬтНтЮіЃКНтЃК(1)ОиаЮЦНУцЭМЕФСНБпГЄЗжБ№ЮЊx mЃЌ![]() mЃЌ
mЃЌ
ИљОнЬтвтЃЌЕУ
НтЕУ![]() ЁмxЁм16.
ЁмxЁм16.
yЃН![]() ЁС400ЃЋ
ЁС400ЃЋ![]() ЁС248ЃЋ16 000
ЁС248ЃЋ16 000
ЃН800xЃЋ![]() ЃЋ16 000ЃЌ
ЃЋ16 000ЃЌ![]() ЁмxЁм16.
ЁмxЁм16.
(2)yЁфЃН800Ѓ![]() ЃЌ
ЃЌ
ЕБ![]() ЁмxЁм16ЪБЃЌyЁфЃМ0ЃЌКЏЪ§дк
ЁмxЁм16ЪБЃЌyЁфЃМ0ЃЌКЏЪ§дк![]() ЩЯЮЊМѕКЏЪ§ЃЌ
ЩЯЮЊМѕКЏЪ§ЃЌ
ЫљвдЕБГЄЮЊ16 mЃЌПэЮЊ12.5 mЪБЃЌзмдьМлyзюЕЭЃЌЮЊ45 000дЊЃЎ

 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ