题目内容
3.应试教育下的高三学生身体素质堪忧,教育部门对某市100名高三学生的课外体育锻炼时间进行调查.他们的课外体育锻炼时间及相应的频数如下表:| 运动时间 (单位:小时) | $[0,\frac{1}{6})$ | $[\frac{1}{6},\frac{1}{3})$ | $[\frac{1}{3},\frac{1}{2})$ | $[\frac{1}{2},\frac{2}{3})$ | $[\frac{2}{3},\frac{5}{6})$ | $[\frac{5}{6},1)$ |
| 总人数 | 10 | 18 | 22 | 25 | 20 | 5 |
(1)根据已知条件完成下面的2×2列联表:
| 课外体育不达标 | 课外体育达标 | 合计 | |
| 男 | |||
| 女 | 10 | 55 | |
| 合计 |
附:${Χ^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
| 参考数据 | 当Χ2≤2.706时,无充分证据判定变量A,B有关联,可以认为两变量无关联; |
| 当Χ2>2.706时,有90%的把握判定变量A,B有关联; | |
| 当Χ2>3.841时,有95%的把握判定变量A,B有关联; | |
| 当Χ2>6.635时,有99%的把握判定变量A,B有关联. |
分析 (1)由所给频数表知,在抽取的100人中,“课外体育达标”的学生有25人,从而可得2×2列联表;
(2)根据公式计算相关指数Χ2的观测值,比较临界值的大小,可判断按95%的可靠性要求,能否认为“课外体育达标”与性别有关.
解答 解:(1)由所给频数表知,在抽取的100人中,“课外体育达标”的学生有25人,从而2×2列联表如下:
| 课外体育不达标 | 课外体育达标 | 合计 | |
| 男 | 30 | 15 | 45 |
| 女 | 45 | 10 | 55 |
| 合计 | 75 | 25 | 100 |
(2)${Χ^2}=\frac{{100×{{(30×10-45×15)}^2}}}{75×25×45×55}=\frac{100}{33}≈3.030<3.841$(17分)(式子列对,计算错误扣3分)
因此没有95%的把握认为“课外体育达标”与性别有关.(18分)
点评 本题考查了列联表及利用列联表进行独立性检验的思想方法,熟练掌握独立性检验的思想方法是解题的关键.

练习册系列答案
相关题目
14.班主任为了对本班学生的考试成绩进行分析,决定从全班25名女同学,15名男同学中随机抽取一个容量为8的样本进行分析.随机抽出8位,他们的数学分数从小到大排序是:60、65、70、75、80、85、90、95,物理分数从小到大排序是:72、77、80、84、88、90、93、95.
(Ⅰ)如果按性别比例分层抽样,男女同学分别抽取多少人?
(Ⅱ)若这8位同学的数学、物理分数对应如下表:
根据上表数据用变量y与x的相关系数或散点图说明物理成绩y与数学成绩x之间是否具有线性相关性?如果具有线性相关性,求y与x的线性回归方程(系数精确到0.01);如果不具有线性相关性,请说明理由.
参考公式:相关系数$r=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sqrt{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}\sqrt{\sum_i^n{({y_i}-\overline y}}{)^2}}}$;回归直线的方程是:$\widehat{y}$=bx+a.
其中对应的回归估计值b=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,a=$\overline{y}$-b$\overline{x}$;
参考数据:$\overline{x}$=77.5,$\overline{y}$=85,$\sum_{i=1}^{8}$(x1-$\overline{x}$)2≈1050,$\sum_{i=1}^{8}$(y1-$\overline{y}$)2≈456;$\sum_{i=1}^{8}$(x1-$\overline{x}$)(y1-$\overline{y}$)≈688,$\sqrt{1050}$≈32.4,$\sqrt{456}$≈21.4,$\sqrt{550}$≈23.5.
(Ⅰ)如果按性别比例分层抽样,男女同学分别抽取多少人?
(Ⅱ)若这8位同学的数学、物理分数对应如下表:
| 学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 数学分数x | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
| 物理分数y | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
参考公式:相关系数$r=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sqrt{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}\sqrt{\sum_i^n{({y_i}-\overline y}}{)^2}}}$;回归直线的方程是:$\widehat{y}$=bx+a.
其中对应的回归估计值b=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,a=$\overline{y}$-b$\overline{x}$;
参考数据:$\overline{x}$=77.5,$\overline{y}$=85,$\sum_{i=1}^{8}$(x1-$\overline{x}$)2≈1050,$\sum_{i=1}^{8}$(y1-$\overline{y}$)2≈456;$\sum_{i=1}^{8}$(x1-$\overline{x}$)(y1-$\overline{y}$)≈688,$\sqrt{1050}$≈32.4,$\sqrt{456}$≈21.4,$\sqrt{550}$≈23.5.
11.设已求出一条直线回归方程为$\widehaty=2-1.5x$,则变量x增加一个单位时( )
| A. | y平均增加1.5个单位 | B. | y平均减少1.5个单位 | ||
| C. | y平均增加2个单位 | D. | y平均减少2个单位 |
18.据气象预报,某地区下月有小洪水的概率为0.2,有大洪水的概率为0.05.该地区某工地上有一台大型设备,两名技术人员就保护设备提出了以下两种方案.
方案一:建一保护围墙,需花费4000元,但围墙无法防止大洪水,当大洪水来临时,设备会受损,损失费为30000元.
方案二:不采取措施,希望不发生洪水,此时小洪水来临将损失15000元,大洪水来临将损失30000元.
以下说法正确的是( )
方案一:建一保护围墙,需花费4000元,但围墙无法防止大洪水,当大洪水来临时,设备会受损,损失费为30000元.
方案二:不采取措施,希望不发生洪水,此时小洪水来临将损失15000元,大洪水来临将损失30000元.
以下说法正确的是( )
| A. | 方案一的平均损失比方案二的平均损失大 | |
| B. | 方案二的平均损失比方案一的平均损失大 | |
| C. | 方案一的平均损失与方案二的平均损失一样大 | |
| D. | 方案一的平均损失与方案二的平均损失无法计算 |
15.已知1,2,3,4,x1,x2,x3的平均数是8,那么x1+x2+x3的值是( )
| A. | 14 | B. | 22 | C. | 32 | D. | 46 |
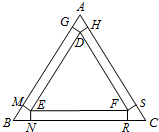 如图:在边长为6米的等边△ABC钢板内,作一个△DEF,使得△DEF的三边到△ABC所对应的三边之间的距离均x(0<x<$\frac{2}{3}$$\sqrt{3}$)米,过点D分别向AB,AC边作垂线,垂足依次为G,H;过点E分别向AB,BC边作垂线,垂足依次为M,N;过点F分别向BC,AC边作垂线,垂足依次为R,S.接着在△ABC的三个内角处,分别沿DG,DH、EM,EN、FR,FS进行切割,割去的三个全等的小四边形分别为AGDH、BMEN、CRFS.然后把矩形GDEM、NEFR、SFDH分别沿DE、EF、FD向上垂直翻折,并对翻折后的钢板进行无缝焊接(注:切割和无缝焊接过程中的损耗和费用忽略不计),从而构成一个无盖的正三棱柱蓄水池.
如图:在边长为6米的等边△ABC钢板内,作一个△DEF,使得△DEF的三边到△ABC所对应的三边之间的距离均x(0<x<$\frac{2}{3}$$\sqrt{3}$)米,过点D分别向AB,AC边作垂线,垂足依次为G,H;过点E分别向AB,BC边作垂线,垂足依次为M,N;过点F分别向BC,AC边作垂线,垂足依次为R,S.接着在△ABC的三个内角处,分别沿DG,DH、EM,EN、FR,FS进行切割,割去的三个全等的小四边形分别为AGDH、BMEN、CRFS.然后把矩形GDEM、NEFR、SFDH分别沿DE、EF、FD向上垂直翻折,并对翻折后的钢板进行无缝焊接(注:切割和无缝焊接过程中的损耗和费用忽略不计),从而构成一个无盖的正三棱柱蓄水池.