Question

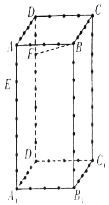
【题目】如图，直三棱柱中， ，，是的中点，△是等腰三角形，为的中点，为上一点．

（1）若∥平面，求；

（2）平面将三棱柱分成两个部分，求较小部分与较大部分的体积之比．

Answer 1

【答案】（1）;（2）

【解析】

试题分析：（1） 取中点为，连结，根据条件∥平面,又有平面平面,这样根据线面平行的性质定理，可得,这样根据平行线的比例可得的值；

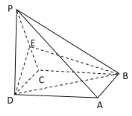
（2）如图，通过割补法将几何体补成三棱柱,那么所求几何体的体积就是,然后再用大的三棱柱的体积减小部分的体积，就是剩下的几何体的体积，再求其比值.

试题解析：取中点为，连结，

∵分别为中点

∴∥∥，∴四点共面，

且平面平面

又平面，且∥平面

∴∥

∵为的中点，

∴是的中点，

∴．

（2）因为三棱柱为直三棱柱，平面，

又，则平面

设，又三角形是等腰三角形，所以.

如图，将几何体补成三棱柱

∴几何体的体积为：

又直三棱柱体积为：

故剩余的几何体棱台的体积为：

∴较小部分的体积与较大部分体积之比为：．