Question

【题目】长方体中，，，，点，分别在，上，，过，的平面与此长方体的面相交，交线围成一个正方形.

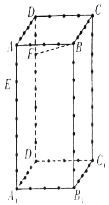
（1）在图中画出这个正方形（不必说明画法和理由）；

（2）求直线与平面所成角的正弦值.

（注：图中未标注名称的点均为线段等分点，仅为（1）中作图提供参考.）

Answer 1

【答案】（1）正方形见解析；（2）.

【解析】

试题分析：（1）利用直线与平面的位置关系可以得出图象；（2）作，垂足为，作，垂足为，可以得到面，进而可得面，因此为直线与平面为成角.

试题解析：（1）交线围成的正方形如图所示.………………（6分）

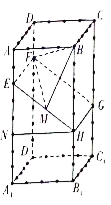
（2）作，垂足为，因为为正方形，

所以，于是.

作，垂足为，连接.

因为，面，

所以面，又面，

因此，又，

所以面.

因此为直线与平面为成角.………………（9分）

，可得，

.

在直角三角形中，.………………（12分）