Question

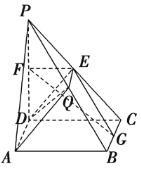
【题目】如图（1）所示，在直角梯形ABCP中，BC∥AP，AB⊥BC，CD⊥AP，AD＝DC＝PD＝2，E、F、G分别为线段PC、PD、BC的中点，现将△PDC折起，使平面PDC⊥平面ABCD（图（2））．

（1）求证：AP∥平面EFG；

（2）若点Q是线段PB的中点，求证：PC⊥平面ADQ；

（3）求三棱锥C－EFG的体积．

Answer 1

【答案】（1）详见解析（2）详见解析（3）

【解析】

试题分析：（1）由条件可得EF∥CD∥AB，利用直线和平面平行的判定定理证得EF∥平面PAB．同理可证，EG∥平面PAB，可得平面EFG∥平面PAB．再利用两个平面平行的性质可得AP∥平面EFG．（2）由条件可得DA、DP、DC互相垂直，故AD⊥平面PCD，AD⊥PC．再由EQ平行且等于BC可得EQ平行且等于AD，故ADEQ为梯形．再根据DE为等腰直角三角形PCD 斜边上的中线，可得DE⊥PC．再利用直线和平面垂直的判定定理证得PC⊥平面ADQ．（3）根据VC-EFG=VG-CEF=S△CEFCG=（EFDF）CG，运算求得结果

试题解析：（1）证明：∵E、F分别是PC，PD的中点，

∴EF∥CD∥AB．

又EF平面PAB，AB平面PAB，∴EF∥平面PAB．

同理，EG∥平面PAB，∴平面EFG∥平面PAB．

又∵AP平面PAB，∴AP∥平面EFG．

（2）解：连接DE，EQ，

∵E、Q分别是PC、PB的中点，∴EQ∥BC∥AD．

∵平面PDC⊥平面ABCD，PD⊥DC，∴PD⊥平面ABCD．

∴PD⊥AD，又AD⊥DC，∴AD⊥平面PDC，∴AD⊥PC．

在△PDC中，PD＝CD，E是PC的中点，

∴DE⊥PC，∴PC⊥平面ADEQ，即PC⊥平面ADQ．

（3）VC－EFG＝VG－CEF＝S△CEF·GC＝××1=