题目内容
13.在△ABC中,∠C=90°,D是BC的中点.若AB=5,AD=$\sqrt{13}$,则sin∠BAD=$\frac{{6\sqrt{13}}}{65}$.分析 作DE⊥AB,垂足为E,利用勾股定理求出BD,由等面积可得DE,即可得出结论.
解答 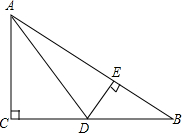 解:作DE⊥AB,垂足为E,则
解:作DE⊥AB,垂足为E,则
设BD=CD=x,则AC=$\sqrt{13-{x}^{2}}$,
∴13-x2+4x2=25,
∴x=2,
由等面积可得$\frac{1}{2}×2×3=\frac{1}{2}×5×DE$,
∴DE=$\frac{6}{5}$,
∴sin∠BAD=$\frac{{6\sqrt{13}}}{65}$.
故答案为:$\frac{{6\sqrt{13}}}{65}$.
点评 本题考查勾股定理、考查三角形面积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
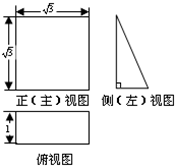
3.某几何体的三视图如图所示,则该几何体的体积为( )
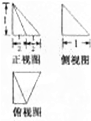

| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
1.i为虚数单位,复数$\frac{{3i-{i^{2014}}}}{1-i}$的化简结果为( )
| A. | 2+i | B. | 1+2i | C. | -1+2i | D. | -2+i |
17. 如图,在边长为2的正方体ABCD-A1B1C1D1中,P、Q分别为棱AB、A1D1的中点,M、N分别为面BCC1B1和DCC1D1上的点,一质点从点P射向点M,遇正方体的面反射(反射服从光的反射原理),反射到点N,再经平面反射,恰好反射至点Q,则三条线段PM、MN、NQ的长度之和为( )
如图,在边长为2的正方体ABCD-A1B1C1D1中,P、Q分别为棱AB、A1D1的中点,M、N分别为面BCC1B1和DCC1D1上的点,一质点从点P射向点M,遇正方体的面反射(反射服从光的反射原理),反射到点N,再经平面反射,恰好反射至点Q,则三条线段PM、MN、NQ的长度之和为( )
 如图,在边长为2的正方体ABCD-A1B1C1D1中,P、Q分别为棱AB、A1D1的中点,M、N分别为面BCC1B1和DCC1D1上的点,一质点从点P射向点M,遇正方体的面反射(反射服从光的反射原理),反射到点N,再经平面反射,恰好反射至点Q,则三条线段PM、MN、NQ的长度之和为( )
如图,在边长为2的正方体ABCD-A1B1C1D1中,P、Q分别为棱AB、A1D1的中点,M、N分别为面BCC1B1和DCC1D1上的点,一质点从点P射向点M,遇正方体的面反射(反射服从光的反射原理),反射到点N,再经平面反射,恰好反射至点Q,则三条线段PM、MN、NQ的长度之和为( )| A. | $\sqrt{22}$ | B. | $\sqrt{21}$ | C. | 2$\sqrt{5}$ | D. | 3$\sqrt{2}$ |
18.某几何体的三视图,如图所示,则该几何体的体积为( )
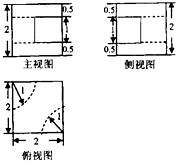

| A. | 8-$\frac{π}{6}$ | B. | 8-$\frac{π}{4}$ | C. | 8-$\frac{π}{3}$ | D. | 8-$\frac{π}{2}$ |