题目内容
2．下列运算结果中，正确的是（ ）| A． | a2a3=a5 | B． | （-a2）3=（-a3）2 | C． | （$\sqrt{a}$-1）0=1 | D． | （-a2）3=a6 |
分析 根据指数幂的运算性质即可求出答案．
解答 解：a2a3=a2+3=a5，
（-a2）3=-a6≠（-a3）2=a6，
（$\sqrt{a}$-1）0=1，若成立，需要满足a≠1，
（-a2）3=-a6，
故正确的是A，
故选：A．
点评 本题考查了指数幂的运算性质，属于基础题．
练习册系列答案
相关题目
17．
如图，在边长为2的正方体ABCD-A1B1C1D1中，P、Q分别为棱AB、A1D1的中点，M、N分别为面BCC1B1和DCC1D1上的点，一质点从点P射向点M，遇正方体的面反射（反射服从光的反射原理），反射到点N，再经平面反射，恰好反射至点Q，则三条线段PM、MN、NQ的长度之和为（ ）
如图，在边长为2的正方体ABCD-A1B1C1D1中，P、Q分别为棱AB、A1D1的中点，M、N分别为面BCC1B1和DCC1D1上的点，一质点从点P射向点M，遇正方体的面反射（反射服从光的反射原理），反射到点N，再经平面反射，恰好反射至点Q，则三条线段PM、MN、NQ的长度之和为（ ）| A． | $\sqrt{22}$ | B． | $\sqrt{21}$ | C． | 2$\sqrt{5}$ | D． | 3$\sqrt{2}$ |
14．某农民在一块耕地上种植一种作物，每年种植成本为800元，此作物的市场价格和这块地上的产量均具有随机性，且互不影响，其具体情况如下表：
（Ⅰ）设X表示该农民在这块地上种植1年此作物的利润，求X的分布列；
（Ⅱ）若在这块地上连续3年种植此作物，求这3年中第二年的利润少于第一年的概率．
| 作物产量（kg） | 300 | 500 |
| 概率 | 0.5 | 0.5 |
| 作物市场价格（元/kg） | 6 | 10 |
| 概率 | 0.6 | 0.4 |
（Ⅱ）若在这块地上连续3年种植此作物，求这3年中第二年的利润少于第一年的概率．
12．某次数学测试后从两个班中各随机的抽取10名学生的数学成绩，作出它们的茎叶图如图所示，已知甲班的中位数为a1，标准差为s1，乙班的中位数为a2，标准差为s2，则由茎叶图可得（ ）
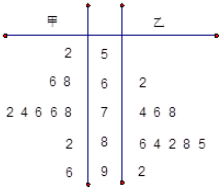
| A． | a1＜a2，s1＞s2 | B． | a1＜a2，s1＜s2 | C． | a1＞a2，s1＞s2 | D． | a1＞a2，s1＜s2 |