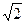题目内容
设圆C满足:(1)截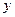 轴所得弦长为2;(2)被
轴所得弦长为2;(2)被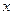 轴分成两段圆弧,其弧长的比为5∶1.
轴分成两段圆弧,其弧长的比为5∶1.
在满足条件(1)、(2)的所有圆中,求圆心到直线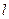 :3
:3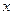 -4
-4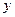 =0的距离最小的圆的方程.
=0的距离最小的圆的方程.
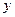 轴所得弦长为2;(2)被
轴所得弦长为2;(2)被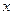 轴分成两段圆弧,其弧长的比为5∶1.
轴分成两段圆弧,其弧长的比为5∶1.在满足条件(1)、(2)的所有圆中,求圆心到直线
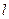 :3
:3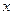 -4
-4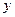 =0的距离最小的圆的方程.
=0的距离最小的圆的方程.圆的方程为
(x-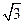 )2+(y-
)2+(y-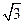 )2=4或(x+
)2=4或(x+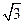 )2+(y+
)2+(y+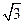 2=4
2=4
(x-
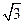 )2+(y-
)2+(y-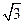 )2=4或(x+
)2=4或(x+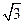 )2+(y+
)2+(y+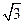 2=4
2=4解:设所求圆的圆心为P( ,
, ),半径为
),半径为 ,则P到
,则P到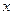 轴、
轴、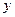 轴的距离分别为|
轴的距离分别为| |、|
|、| |.
|.
由题设圆P截x轴所得劣弧所对圆心角为60°……2分,圆P截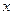 轴所得弦长为
轴所得弦长为 ,故 3
,故 3 2=4
2=4 2,
2,
又圆P截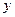 轴所得弦长为2,所以有r2=
轴所得弦长为2,所以有r2= 2+1,…………5分
2+1,…………5分
从而有4 2-3
2-3 2=3
2=3
又点P( ,
, )到直线3
)到直线3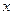 -4
-4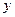 =0距离为
=0距离为 =
= ,…………7分
,…………7分
所以25 2=|3
2=|3 -4
-4 |2
|2
=9 2+16
2+16 2-24
2-24
 ≥9
≥9 2+16
2+16 2-12(
2-12( 2+
2+ 2)………10分
2)………10分
=4b2-3 2=3
2=3
当且仅当 =
= 时上式等号成立,此时25
时上式等号成立,此时25 2=3,从而
2=3,从而 取得最小值,
取得最小值,
由此有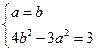 ,解方程得
,解方程得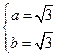 或
或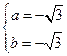 ………12分
………12分
由于3 2=4
2=4 2,知
2,知 =2,于是所求圆的方程为
=2,于是所求圆的方程为
(x-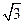 )2+(y-
)2+(y-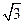 )2=4或(x+
)2=4或(x+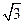 )2+(y+
)2+(y+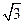 2=4……….13分
2=4……….13分
 ,
, ),半径为
),半径为 ,则P到
,则P到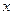 轴、
轴、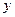 轴的距离分别为|
轴的距离分别为| |、|
|、| |.
|.由题设圆P截x轴所得劣弧所对圆心角为60°……2分,圆P截
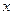 轴所得弦长为
轴所得弦长为 ,故 3
,故 3 2=4
2=4 2,
2,又圆P截
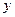 轴所得弦长为2,所以有r2=
轴所得弦长为2,所以有r2= 2+1,…………5分
2+1,…………5分从而有4
 2-3
2-3 2=3
2=3又点P(
 ,
, )到直线3
)到直线3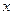 -4
-4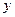 =0距离为
=0距离为 =
= ,…………7分
,…………7分 所以25
 2=|3
2=|3 -4
-4 |2
|2=9
 2+16
2+16 2-24
2-24
 ≥9
≥9 2+16
2+16 2-12(
2-12( 2+
2+ 2)………10分
2)………10分=4b2-3
 2=3
2=3当且仅当
 =
= 时上式等号成立,此时25
时上式等号成立,此时25 2=3,从而
2=3,从而 取得最小值,
取得最小值,由此有
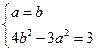 ,解方程得
,解方程得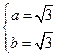 或
或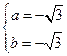 ………12分
………12分由于3
 2=4
2=4 2,知
2,知 =2,于是所求圆的方程为
=2,于是所求圆的方程为(x-
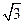 )2+(y-
)2+(y-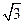 )2=4或(x+
)2=4或(x+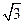 )2+(y+
)2+(y+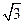 2=4……….13分
2=4……….13分
练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
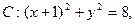 定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足
定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足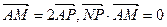 ,点N的轨迹为曲线E。
,点N的轨迹为曲线E。  于G、H不同的两点,求此直线斜率的取值范围。
于G、H不同的两点,求此直线斜率的取值范围。
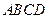 的两条对角线相交于点
的两条对角线相交于点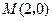 ,
,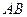 边所在直线的方程为
边所在直线的方程为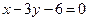 , 点
, 点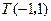 在
在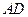 边所在直线上.
边所在直线上.
 ,其中
,其中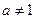 ,且
,且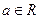 .
.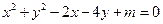 ;
;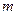 的取值范围;
的取值范围;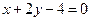 相交于
相交于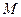 、
、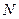 两点且
两点且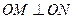
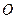 为坐标原点),求
为坐标原点),求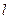 过点
过点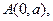 斜率为1,圆
斜率为1,圆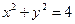 上恰有1个点到
上恰有1个点到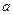 的值为( )
的值为( )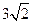

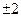
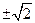
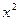 +
+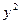 -4
-4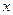 +3=0上的动点,则点P到直线
+3=0上的动点,则点P到直线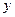 +1=0的距离的
+1=0的距离的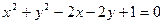 上的点到直线
上的点到直线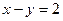 的距离的最大值是__________________
的距离的最大值是__________________ 与圆
与圆 相交与P,Q两点,且此圆被分成的两段弧长之比为1:2,则
相交与P,Q两点,且此圆被分成的两段弧长之比为1:2,则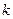 的值为( )
的值为( )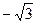 或
或
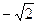 或
或