Question

【题目】已知函数f（x）=ex ， x∈R．
（1）若直线y=kx+1与f （x）的反函数g（x）=lnx的图象相切，求实数k的值；
（2）设x＞0，讨论曲线y=f （x） 与曲线y=mx2（m＞0）公共点的个数．
（3）设a＜b，比较 与 的大小，并说明理由．

Answer 1

【答案】
（1）解：函数f（x）=ex的反函数为g（x）=lnx，∴ ．

设直线y=kx+1与g（x）的图象相切于点P（x0，y0），则 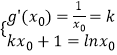，解得 ，k=e﹣2，

∴k=e﹣2．

（2）解：当x＞0，m＞0时，令f（x）=mx2，化为m= ，

令h（x）= ，则 ，

则x∈（0，2）时，h′（x）＜0，h（x）单调递减；x∈（2，+∞）时，h′（x）＞0，h（x）单调递增．

∴当x=2时，h（x）取得极小值即最小值， ．

∴当 时，曲线y=f （x） 与曲线y=mx2（m＞0）公共点的个数为0；

当 时，曲线y=f （x） 与曲线y=mx2（m＞0）公共点的个数为1；

当 时，曲线y=f （x） 与曲线y=mx2（m＞0）公共点个数为2．

（3）解： =

=

= ，

令g（x）=x+2+（x﹣2）ex（x＞0），则g′（x）=1+（x﹣1）ex．

g′′（x）=xex＞0，∴g′（x）在（0，+∞）上单调递增，且g′（0）=0，

∴g′（x）＞0，∴g（x）在（0，+∞）上单调递增，

而g（0）=0，∴在（0，+∞）上，有g（x）＞g（0）=0．

∵当x＞0时，g（x）=x+2+（x﹣2）ex＞0，且a＜b，

∴ ，

即当a＜b时， ．

【解析】（1）先求出其反函数，利用导数得出切线的斜率即可；（2）由f（x）=mx2 ， 令h（x）= ，利用导数研究函数h（x）的单调性即可得出；（3）利用作差法得 = = = ，令g（x）=x+2+（x﹣2）ex（x＞0），利用导数研究其单调性即可证明．