Question

【题目】如图，某校有一块形如直角三角形ABC的空地，其中∠B为直角，AB长40米，BC长50米，现欲在此空地上建造一间健身房，其占地形状为矩形，且B为矩形的一个顶点，求该健身房的最大占地面积．

Answer 1

【答案】解：如图，设矩形为EBFP，FP长为x米，其中0＜x＜40，
健身房占地面积为y平方米．因为△CFP∽△CBA，
以 ， ，求得BF=50﹣ ，
从而y=BFFP=（50﹣ ）x
=﹣
=﹣
≤500．
当且仅当x=20时，等号成立．
答：该健身房的最大占地面积为500平方米．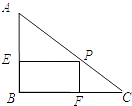

【解析】设出矩形的边FP的边长，利用三角形相似求出矩形的宽，表示出矩形面积，利用二次函数的最值求解即可．
【考点精析】通过灵活运用二次函数在闭区间上的最值，掌握当时，当时，；当时在上递减，当时，即可以解答此题．