题目内容
【题目】如图,在直三棱柱ABC﹣A1B1C1中,三角形ABC为等腰直角三角形,AC=BC= ![]() ,AA1=1,点D是AB的中点.
,AA1=1,点D是AB的中点. 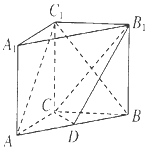
(1)求证:AC1∥平面CDB1;
(2)二面角B1﹣CD﹣B的平面角的大小.
【答案】
(1)证明:在直三棱柱ABC﹣A1B1C1中,
设BC1∩B1C=E,则E为BC1的中点,连接ED
∵D为AB的中点,∴ED∥AC
又∵ED平面CDB1,AC1平面CDB1,
∴AC1∥平面CDB1
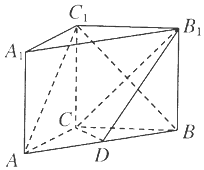
(2)解:∵△ABC中,AC=BC,D为AB中点,∴CD⊥AB,
又∵BB1⊥平面ABC,CD平面ABC,∴BB1⊥CD,
又AB∩BB1=B,∴CD⊥平面ABB1A1,
∵B1D平面ABB1A1,AB平面ABB1A1
∴CD⊥B1D,CD⊥AB,
∴∠B1DB为二面角B1﹣CD﹣B的平面角
∵三角形ABC中,AB=2,∴BD=1,
在Rt△B1BD中, ![]() ,
,
∴∠B1BD=45°,
∴二面角B1﹣CD﹣B的平面角的大小为45°
【解析】(1)设BC1∩B1C=E,连接ED,则ED∥AC,由此能证明AC1∥平面CDB1 . (2)推导出CD⊥AB,BB1⊥CD,从而CD⊥平面ABB1A1 , 进而CD⊥B1D,CD⊥AB,∠B1DB为二面角B1﹣CD﹣B的平面角,由此能求出二面角B1﹣CD﹣B的平面角的大小.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目