题目内容
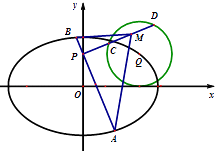
【题目】如图,椭圆![]() 的离心率为
的离心率为![]() ,其左顶点
,其左顶点![]() 在圆
在圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 与椭圆
与椭圆![]() 的另一个交点为
的另一个交点为![]() ,与圆
,与圆![]() 的另一个交点为
的另一个交点为![]() .
.
(ⅰ)当![]() 时,求直线
时,求直线![]() 的斜率;
的斜率;
(ⅱ)是否存在直线![]() ,使
,使![]() ?若存在,求出直线
?若存在,求出直线![]() 的斜率;若不存在,说明理由.
的斜率;若不存在,说明理由.
【答案】(1)![]() ;(2)(ⅰ)1,-1;(ⅱ)不存在直线
;(2)(ⅰ)1,-1;(ⅱ)不存在直线![]() ,使得
,使得![]() .
.
【解析】
试题分析:(1)要求椭圆标准方程,就要知道两个独立条件,椭圆左顶点在圆![]() 说明
说明![]() ,再由离心率可得
,再由离心率可得![]() ,最后由
,最后由![]() 可得
可得![]() ;(2)本题考查解析几何的基本方法,直线与椭圆相交问题与存在性命题,解决方法是(ⅰ)设点
;(2)本题考查解析几何的基本方法,直线与椭圆相交问题与存在性命题,解决方法是(ⅰ)设点![]() ,显然直线
,显然直线![]() 存在斜率,设直线
存在斜率,设直线![]() 的方程为
的方程为![]() ,与椭圆方程联立并代入消元得
,与椭圆方程联立并代入消元得![]() ,其中一个根是-4,另一根设为
,其中一个根是-4,另一根设为![]() (易得),再由弦长公式
(易得),再由弦长公式![]() 可求得
可求得![]() ;(ⅱ)圆中的弦长
;(ⅱ)圆中的弦长![]() 利用垂径定理求得,把
利用垂径定理求得,把![]() 代入方程
代入方程![]() ,解之,如能解得
,解之,如能解得![]() 值,说明存在,如方程无解,说明不存在.
值,说明存在,如方程无解,说明不存在.
试题解析:(1)因为椭圆![]() 的左顶点
的左顶点![]() 在圆
在圆![]() 上,所以
上,所以![]() ,
,
又离心率为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
所以![]() ,所以
,所以![]() 的方程为
的方程为![]() .
.
(2)(ⅰ)设点![]() ,显然直线
,显然直线![]() 存在斜率,
存在斜率,
设直线![]() 的方程为
的方程为![]() ,与椭圆方程联立得
,与椭圆方程联立得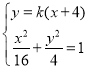 ,
,
化简得到![]() ,
,
因为-4为上面方程的一个根,所以![]() ,
,
所以![]() ,
,
由![]() ,
,
代入得到![]() ,解得
,解得![]() ,所以直线
,所以直线![]() 的斜率为1,-1.
的斜率为1,-1.
(ⅱ)圆心到直线![]() 的距离为
的距离为![]() ,
,![]() ,
,
因为![]() ,
,
代入得到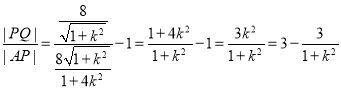 ,
,
显然,![]() ,所以不存在直线
,所以不存在直线![]() ,使得
,使得![]() .
.

练习册系列答案
相关题目