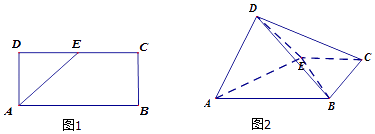
题目内容
【题目】如图①,在矩形![]() 中,
中, ![]() ,
, ![]() 是
是![]() 的中点,将三角形
的中点,将三角形![]() 沿
沿![]() 翻折到图②的位置,使得平面
翻折到图②的位置,使得平面![]()
![]() 平面
平面![]() .
.
(1)在线段![]() 上确定点
上确定点![]() ,使得
,使得![]() 平面
平面![]() ,并证明;
,并证明;
(2)求![]() 与
与![]() 所在平面构成的锐二面角的正切值.
所在平面构成的锐二面角的正切值.

【答案】(1)详见解析;(2) ![]() .
.
【解析】试题分析:证明线面平行利用线面平行的判定定理,本题借助平行四边形可以得到线线平行,进而证明线面平行;求二面角一是传统方法,“一作,二证,三求”,本题采用传统方法利用线面垂直做出二面角,然后求出二面角,二是建立空间直角坐标系,借助空间向量,求法向量,利用公式求角.
试题解析:
(Ⅰ)点![]() 是线段
是线段![]() 中点时,
中点时, ![]() 平面
平面![]() .
.
证明:记![]() ,
, ![]() 的延长线交于点
的延长线交于点![]() ,因为
,因为![]() ,所以点
,所以点![]() 是
是![]() 的中点,所以
的中点,所以![]() .
.
而![]() 在平面
在平面![]() 内,
内, ![]() 在平面
在平面![]() 外,所以
外,所以![]() 平面
平面![]() .
.
(Ⅱ)在矩形![]() 中,
中, ![]() ,
, ![]() ,
,
因为平面![]()
![]() 平面
平面![]() ,且交线是
,且交线是![]() ,所以
,所以![]()
![]() 平面
平面![]() .
.
在平面![]() 内作
内作![]()
![]()
![]() ,连接
,连接![]() ,则
,则![]()
![]()
![]() .
.
所以![]() 就是
就是![]() 与
与![]() 所在平面构成的锐二面角的平面角.
所在平面构成的锐二面角的平面角.
因为![]() ,
, ![]() ,所以
,所以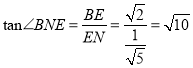 .
.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目