题目内容
10.已知向量$\overrightarrow{a}$=(4,3),$\overrightarrow{b}$=(-1,2).(1)求$\overrightarrow{a}$与$\overrightarrow{b}$的夹角的余弦值;
(2)若向量$\overrightarrow{a}$-λ$\overrightarrow{b}$与2$\overrightarrow{a}$+$\overrightarrow{b}$平行,求λ的值.
分析 (1)直接利用向量的数量积求$\overrightarrow{a}$与$\overrightarrow{b}$的夹角的余弦值;
(2)表示出向量$\overrightarrow{a}$-λ$\overrightarrow{b}$,2$\overrightarrow{a}$+$\overrightarrow{b}$,利用两者平行的充要条件,露垂芳草,即可求λ的值.
解答 (本小题满分12分)
解:(1)∵向量$\overrightarrow{a}$=(4,3),$\overrightarrow{b}$=(-1,2).
∴$\overrightarrow{a}•\overrightarrow{b}$=-4+6=2,$\left|\overrightarrow{a}\right|$=$\sqrt{{4}^{2}+{3}^{2}}$=5,$\left|\overrightarrow{b}\right|$=$\sqrt{(-1)^{2}+{2}^{2}}$=$\sqrt{5}$…(3分)
∴cos$<\overrightarrow{a},\overrightarrow{b}>$=$\frac{\overrightarrow{a}•\overrightarrow{b}}{\left|\overrightarrow{a}\right|\left|\overrightarrow{b}\right|}$=$\frac{2}{5\sqrt{5}}$=$\frac{2\sqrt{5}}{25}$.…(6分)
(2)∵向量$\overrightarrow{a}$=(4,3),$\overrightarrow{b}$=(-1,2).向量$\overrightarrow{a}$-λ$\overrightarrow{b}$=(4+λ,3-2λ),2$\overrightarrow{a}$+$\overrightarrow{b}$=(7,8)…(8分)
∵向量$\overrightarrow{a}$-λ$\overrightarrow{b}$与2$\overrightarrow{a}$+$\overrightarrow{b}$平行,
∴$\frac{4+λ}{7}=\frac{3-2λ}{8}$,…(10分)
解得:λ=$-\frac{1}{2}$.…(12分)
点评 本题考查平面向量数量积的应用,向量共线以及向量的夹角的求法,考查计算能力.

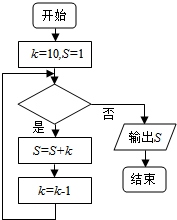 若如框图所给的程序运行结果为S=28,那么判断框中应填入的条件是( )
若如框图所给的程序运行结果为S=28,那么判断框中应填入的条件是( )| A. | k<7? | B. | k≤7? | C. | k>7? | D. | k≥7? |
| A. | a2<ab | B. | |a|<|b| | C. | $\frac{1}{a}>\frac{1}{b}$ | D. | ${({\frac{1}{2}})^a}<{({\frac{1}{2}})^b}$ |