题目内容
13.已知椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1与x轴、y轴的正半轴分别交于A、B两点,左焦点为F,求△ABF的面积.分析 由椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1,可得a=5,b=4,c=3,所以|AF|=a+c=8,|OB|=4,即可求出△ABF的面积.
解答 解:由椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1,可得a=5,b=4,c=3,
∴|AF|=a+c=8,|OB|=4,
∴△ABF的面积为$\frac{1}{2}×8×4$=16.
点评 本题考查椭圆的方程与性质,考查三角形的面积的计算,确定椭圆的几何量是关键.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
18.线段P1P2长为5cm,点P在P1P2的延长线上,且|P2P|=5cm,则点P分$\overrightarrow{{P}_{2}{P}_{1}}$所成的比是( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |
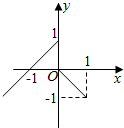 (1)已知y=f(x)的图象如图所示,求f(x);
(1)已知y=f(x)的图象如图所示,求f(x);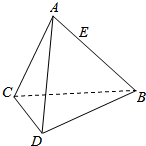 如图,棱长为4的正四面体ABCD,AE=$\frac{1}{3}$AB,试建立适当的坐标系,写出各点的坐标.
如图,棱长为4的正四面体ABCD,AE=$\frac{1}{3}$AB,试建立适当的坐标系,写出各点的坐标.