题目内容
2．求函数f（x）=$\sqrt{{x}^{2}+4}$+$\sqrt{{x}^{2}-10x+34}$的最小值．分析 化简函数f（x）=$\sqrt{{x}^{2}+4}$+$\sqrt{{x}^{2}-10x+34}$=$\sqrt{{x}^{2}+4}$+$\sqrt{（x-5）^{2}+{3}^{2}}$，从而可得其几何意义是点（x，0）到点（0，-2），（5，3）的距离之和，从而求最小值．
解答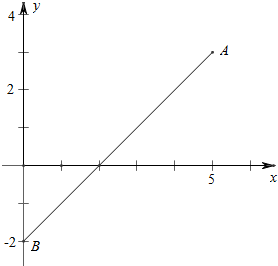 
解：∵函数f（x）=$\sqrt{{x}^{2}+4}$+$\sqrt{{x}^{2}-10x+34}$
=$\sqrt{{x}^{2}+4}$+$\sqrt{（x-5）^{2}+{3}^{2}}$，
故其几何意义是点（x，0）到点（0，-2），（5，3）的距离之和，
则函数f（x）=$\sqrt{{x}^{2}+4}$+$\sqrt{{x}^{2}-10x+34}$的最小值为
$\sqrt{{5}^{2}+（3+2）^{2}}$=5$\sqrt{2}$．
点评 本题考查了函数解析式的化简与其几何意义的应用，属于中档题．
练习册系列答案
补充习题江苏系列答案
学练快车道口算心算速算天天练系列答案
相关题目