题目内容
【题目】已知函数![]() (
(![]() 为常数)
为常数)
(Ⅰ)若![]() 是定义域上的单调函数,求
是定义域上的单调函数,求![]() 的取值范围;
的取值范围;
(Ⅱ)若![]() 存在两个极值点
存在两个极值点![]() ,且
,且![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(Ⅰ) ![]() ;(Ⅱ)
;(Ⅱ) ![]() 。
。
【解析】
(Ⅰ)由![]() 是单调函数可得
是单调函数可得![]() 在定义域上恒成立,然后转化为二次方程根的分布的问题处理即可.(Ⅱ)由题意得
在定义域上恒成立,然后转化为二次方程根的分布的问题处理即可.(Ⅱ)由题意得![]() 是方程
是方程![]() 的两根,故得
的两根,故得![]() ,不妨令
,不妨令![]() ,然后将
,然后将![]() 表示为
表示为![]() 的函数,最后根据函数的单调性可求得最大值.
的函数,最后根据函数的单调性可求得最大值.
(Ⅰ)∵![]() ,
,![]() ,
,
∴![]() .
.
设![]() ,
,![]() ,
,
∵![]() 是定义域上的单调函数,函数
是定义域上的单调函数,函数![]() 的图象为开口向上的抛物线,
的图象为开口向上的抛物线,
∴![]() 在定义域上恒成立,即
在定义域上恒成立,即![]() 在
在![]() 上恒成立.
上恒成立.
又二次函数图象的对称轴为![]() ,且图象过定点
,且图象过定点![]() ,
,
∴![]() ,或
,或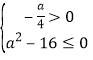 ,解得
,解得![]() .
.
∴实数![]() 的取值范围为
的取值范围为![]() .
.
(Ⅱ)由(I)知函数![]() 的两个极值点
的两个极值点![]() 满足
满足![]() ,
,
所以![]() ,
,
不妨设![]() ,则
,则![]() 在
在![]() 上是减函数,
上是减函数,
∴![]() ,
,
∴![]()
![]()
![]()
![]()
![]()
![]() .
.
令![]() ,则
,则![]() ,
,
又![]() ,即
,即![]() ,
,
解得![]() ,
,
故![]() ,
,
∴![]() .
.
设![]() ,
,
则![]() ,
,
∴![]() 在
在![]() 上为增函数.
上为增函数.
∴![]() ,
,
即![]() .
.
所以![]() 的最大值为
的最大值为![]() .
.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目