题目内容
【题目】
为椭圆
上的点，
是两焦点，若
，则
的面积是（ ）
A. 
B. 
C. 
D. 
【答案】A
【解析】
由题意得，在△F1PF2中，∠F1PF2＝60°，|F1P|+|PF2|＝
＝
，|F1F2|＝4，利用余弦定理可求得|F1P||PF2|的值，从而可求得△PF1F2的面积．
∵椭圆
，∴
＝
，b＝2，c＝2．又∵P为椭圆上一点，∠F1PF2＝60°，
且F1、F2为左右焦点，由椭圆的定义得|F1P|+|PF2|＝＝，|F1F2|＝4，
∴|F1F2|2＝|PF1|
+|PF2|-2|PF1||PF2|cos60°
=（|PF1|+|PF2|）2﹣2|PF1||PF2|﹣2|F1P||PF2|cos60°
＝32﹣3|F1P||PF2|
＝16
∴|F1P||PF2|＝
，∴
＝
|PF1||PF2|sin60°＝××
＝
．
故选：A．
小学教材全测系列答案
小学数学口算题卡脱口而出系列答案
优秀生应用题卡口算天天练系列答案
浙江之星课时优化作业系列答案【题目】市场份额又称市场占有率，它在很大程度上反映了企业的竞争地位和盈利能力，是企业非常重视的一个指标.近年来，服务机器人与工业机器人以迅猛的增速占领了中国机器人领域庞大的市场份额，随着“一带一路”的积极推动，包括机器人产业在内的众多行业得到了更广阔的的发展空间，某市场研究人员为了了解某机器人制造企业的经营状况，对该机器人制造企业2017年1月至6月的市场份额进行了调查，得到如下资料：
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
市场份额 | 11 | 163 | 16 | 15 | 20 | 21 |
请根据上表提供的数据，用最小二乘法求出
关于
的线性回归方程，并预测该企业2017年7月份的市场份额.
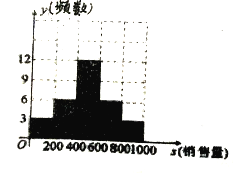
如图是该机器人制造企业记录的2017年6月1日至6月30日之间的产品销售频数（单位：天）统计图.设销售产品数量为
，经统计，当
时，企业每天亏损约为200万元；
当
时，企业平均每天收入约为400万元；
当
时，企业平均每天收入约为700万元.
①设该企业在六月份每天收入为
，求
的数学期望；
②如果将频率视为概率，求该企业在未来连续三天总收入不低于1200万元的概率.
附：回归直线的方程是
，其中
， 
，
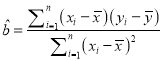【题目】由于往届高三年级数学学科的学习方式大都是“刷题一讲题一再刷题”的模式，效果不理想，某市一中的数学课堂教改采用了“记题型一刷题一检测效果”的模式，并记录了某学生的记题型时间
（单位：
）与检测效果
的数据如下表所示.
记题型时间 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
检测效果 | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
（1）据统计表明，与之间具有线性相关关系，请用相关系数
加以说明（若
，则认为与有很强的线性相关关系，否则认为没有很强的线性相关关系）；
（2）建立关于的回归方程，并预测该学生记题型的检测效果；
（3）在该学生检测效果不低于3.6的数据中任取2个，求检测效果均高于4.4的概率.
参考公式：回归直线
中斜率和截距的最小二乘估计分别为
，
，相关系数
参考数据：
，
，
，
.