题目内容
【题目】由于往届高三年级数学学科的学习方式大都是“刷题一讲题一再刷题”的模式，效果不理想，某市一中的数学课堂教改采用了“记题型一刷题一检测效果”的模式，并记录了某学生的记题型时间
（单位：
）与检测效果
的数据如下表所示.
记题型时间 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
检测效果 | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
（1）据统计表明，与之间具有线性相关关系，请用相关系数
加以说明（若
，则认为与有很强的线性相关关系，否则认为没有很强的线性相关关系）；
（2）建立关于的回归方程，并预测该学生记题型的检测效果；
（3）在该学生检测效果不低于3.6的数据中任取2个，求检测效果均高于4.4的概率.
参考公式：回归直线
中斜率和截距的最小二乘估计分别为
，
，相关系数
参考数据：
，
，
，
.
【答案】（1）
，
与
有很强的线性相关关系.（2）关于的回归方程为
，预测值为
（3）
【解析】
（1）求出相关系数即可得解；
（2）由图表信息求出关于的回归方程；
（3）先求出各种情况的基本事件的个数，再利用古典概型的概率求法，运算即可得解.
（1）由题得
，
，
所以，
所以与有很强的线性相关关系.
（2）由（1）可得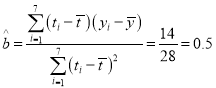
，
所以
，
所以关于的回归方程为.
当
时，
，
所以预测该学生记题型
的检测效果约为6.3.
（3）由题知该学生检测效果不低于3.6的数据有5个，任取2个数据有
，
，
，
，
，
，
，
，
，
共10种情况，其中检测效果均高于4.4的有，
，
，共3种结果，
故所求概率为.
练习册系列答案
发散思维新课堂系列答案
相关题目
