Question

【题目】设集合为下述条件的函数的集合：①定义域为；②对任意实数，都有．

（1）判断函数是否为中元素，并说明理由；

（2）若函数是奇函数，证明：；

（3）设和都是中的元素，求证：也是中的元素，并举例说明，不一定是中的元素．

Answer 1

【答案】（1）为中元素，理由见解析；（2）详见解析；（3）详见解析

【解析】

（1）函数的定义域为，运用作差法结合新定义，可判断出满足条件，即可得到结论；

（2）根据，得到当时，，即可得证；

（3）分别讨论对应点都在或上、分别在两个函数上两种情况，可验证出结论；举例，，取，，可验证出不符合条件，即可得到结论．

（1）函数的定义域为，满足条件①

，，

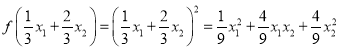即：，满足条件②

函数是中元素

（2）为奇函数，

若当时，

则，

，不满足条件②，

（3）①若对应的点在或图象上

都是中的元素

，

可知结论必然成立

②若对应的点一个在上，一个在上

或

题设结论成立

综上所述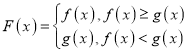：是中元素

当，，满足均为中元素

当时，；当时，

取，

，

又，

存在不满足条件的情况，不一定为中的元素