题目内容
【题目】已知函数![]() 的导函数为
的导函数为![]() ,且对任意的实数
,且对任意的实数![]() 都有
都有![]() (
(![]() 是自然对数的底数),且
是自然对数的底数),且![]() ,若关于
,若关于![]() 的不等式
的不等式![]() 的解集中恰有两个整数,则实数
的解集中恰有两个整数,则实数![]() 的取值范围是
的取值范围是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
利用导数研究其单调性极值与最值并且画出图象即可得出.
∵f'(x)=e﹣x(2x+3)﹣f(x),
∴ex[f(′x)+f(x)]=2x+3,
∴exf(x)=x2+3x+c,
∵f(0)=1,
∴1=0+0+c,
解得c=1
∴f(x)=(x2+3x+1)e﹣x,
∴f′(x)=﹣(x2+x﹣2)e﹣x=﹣(x﹣1)(x+2)e﹣x.
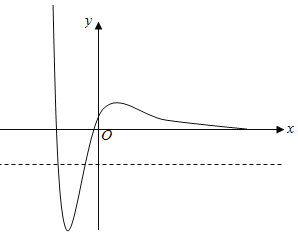
令f′(x)=0,解得x=1或x=﹣2,
当x<﹣2或x>1时,f′(x)<0,函数f(x)单调递减,
当﹣2<x<1时,f′(x)>0,函数f(x)单调递减增,
可得:x=1时,函数f(x)取得极大值,x=﹣2时,函数f(x)取得极小值,
∵f(1)=![]() ,f(﹣2)=﹣e2<0,f(﹣1)=﹣e,f(0)=1>0,f(﹣3)=e3>0
,f(﹣2)=﹣e2<0,f(﹣1)=﹣e,f(0)=1>0,f(﹣3)=e3>0
∴﹣e<m≤0时,f(x)﹣m<0的解集中恰有两个整数恰有两个整数﹣1,﹣2.
故m的取值范围是(﹣e,0],
故选:A.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
【题目】通过随机询问50名性别不同的大学生是否爱好某项运动,得到如下的列联表,由![]() 得
得![]() 参照附表,得到的正确结论是( )
参照附表,得到的正确结论是( )
爱好 | 不爱好 | 合计 | |
男生 | 20 | 5 | 25 |
女生 | 10 | 15 | 25 |
合计 | 30 | 20 | 50 |
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |
A.有99.5%以上的把握认为“爱好该项运动与性别有关”
B.有99.5%以上的把握认为“爱好该项运动与性别无关”
C.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
D.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”

