题目内容
3.先化简,再求代数式(a-1+$\frac{2}{a+1}$)÷(a2+1)的值,其中a=$\sqrt{2}$-1.分析 直接利用代数式的运算法则化简求解,然后代入数值计算即可.
解答 解:(a-1+$\frac{2}{a+1}$)÷(a2+1)
=$\frac{{a}^{2}+1}{a+1}×\frac{1}{{a}^{2}+1}$
=$\frac{1}{a+1}$,
a=$\sqrt{2}$-1,
则$\frac{1}{a+1}$=$\frac{1}{\sqrt{2}-1+1}$=$\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$.
点评 本题考查代数式的化简求值,基本知识的考查.

练习册系列答案
相关题目
13.已知i是虚数单位,若(-1-2i)z=1-i则$\overline z$在复平面上所代表的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
11.已知复数z满足(1-i)z=i2015(其中i为虚数单位),则$\overline{z}$的虚部为( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$i | D. | -$\frac{1}{2}$i |
18.下列说法正确的是( )?
| A. | 一组数据2,5,3,1,4,3的中位数是3 | |
| B. | 五边形的外角和是540度 | |
| C. | “菱形的对角线互相垂直”的逆命题是真命题 | |
| D. | 三角形的外心是这个三角形三条角平分线的交点 |
8.已知不等式组$\left\{\begin{array}{l}{x≤2}\\{y≥1}\\{x-y≥0}\end{array}\right.$的解集记为D,则对?(x,y)∈D使得2x-y取最大值时的最优解是( )
| A. | (2,1) | B. | (2,2) | C. | 3 | D. | 4 |
15.sin135°cos(-15°)+cos225°sin15°等于( )
| A. | -$\frac{\sqrt{3}}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
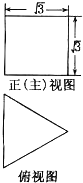 一个底面为正三角形的直三棱柱的正视图和俯视图(单位:cm)如图所示,则它的外接球的表面积等于$\frac{25π}{3}$cm2.
一个底面为正三角形的直三棱柱的正视图和俯视图(单位:cm)如图所示,则它的外接球的表面积等于$\frac{25π}{3}$cm2.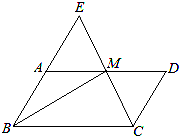 已知:如图,在平行四边形ABCD中,点M在边AD上,且AM=DM.CM、BA的延长线相交于点E.求证:
已知:如图,在平行四边形ABCD中,点M在边AD上,且AM=DM.CM、BA的延长线相交于点E.求证: